题目内容
4.AP、BP分别切⊙O于点A、B,∠P=60°,点C是圆上一动点,则∠C度数为120°或60°.分析 首先根据切线的性质可以得到∠OAP=∠OBP=90°,利用四边形的内角和定理求得∠AOB的度数,然后利用圆周角定理求解.
解答 解:当点C在劣弧上时,
∵AP、BP分别切⊙O于点A、B,
∴∠OAP=∠OBP=90°,
∴∠AOB=360°-60°-90°-90°=120°,
∴∠C=$\frac{1}{2}$∠AOB=60°.
当点C在优弧上时,
∠C=180°-60°=120°.
故答案为:120°或60°.
点评 本题是切线的性质、圆周角定理以及四边形的内角和定理的综合应用,正确理解切线的性质定理是关键.

练习册系列答案
相关题目
19.下列说法:
①有理数包括正有理数和负有理数;
②a为任意有理数,|a|+1总是正数;
③绝对值等于本身的数是0和1;
④(-1)2015=-2015
⑤若a2=(-3)2,则a=-3.
其中错误的有( )
①有理数包括正有理数和负有理数;
②a为任意有理数,|a|+1总是正数;
③绝对值等于本身的数是0和1;
④(-1)2015=-2015
⑤若a2=(-3)2,则a=-3.
其中错误的有( )
| A. | 5个 | B. | 4个 | C. | 3个 | D. | 2个 |
4.已知x2+4-4x+y2+2xy-4y=0,则x+y=( )
| A. | -2 | B. | 4 | C. | 2 | D. | -4 |
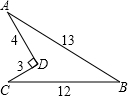 如图所示,某开发区有一块绿地ABCD,AD=3m,CD=4m,∠ADC=90°,CB=12,AB=13m,求这块绿地的面积.
如图所示,某开发区有一块绿地ABCD,AD=3m,CD=4m,∠ADC=90°,CB=12,AB=13m,求这块绿地的面积.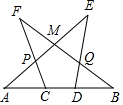 如图,A、C、D、B四点共线,AC=BD,∠A=∠B,∠E=∠F,图中全等三角形有( )对.
如图,A、C、D、B四点共线,AC=BD,∠A=∠B,∠E=∠F,图中全等三角形有( )对. 如图,∠A+∠B+∠C+∠D+∠E+∠F=360°.
如图,∠A+∠B+∠C+∠D+∠E+∠F=360°. 如图,⊙O的直径为5,△ABC为⊙O的内接三角形,CD⊥AB于D,AC=2$\sqrt{6}$,求sin∠BCD的值.
如图,⊙O的直径为5,△ABC为⊙O的内接三角形,CD⊥AB于D,AC=2$\sqrt{6}$,求sin∠BCD的值.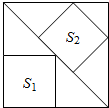 如图,边长为6的大正方形中有两个小正方形,若两个小正方形的面积分别为S1、S2,则S1+S2的值为17.
如图,边长为6的大正方形中有两个小正方形,若两个小正方形的面积分别为S1、S2,则S1+S2的值为17.