题目内容
14.关于x的一元二次方程8x2-(m-1)x+m-7=0(1)m为何值时,方程有一个根为0.
(2)m为何值时,方程的两个根互为相反数?并求出这两个根.
分析 (1)将x=0代入原方程即可得出关于m的一元一次方程,解之即可得出结论;
(2)由方程的两根互为相反数结合根与系数的关系即可得出x1+x2=-$\frac{-(m-1)}{8}$=0,解之即可得出m的值,将m代入原方程,解方程即可得出结论.
解答 解:(1)将x=0代入原方程得:m-7=0,
解得:m=7.
∴m为7时,方程有一个根为0.
(2)∵方程8x2-(m-1)x+m-7=0的两个根互为相反数,
∴x1+x2=-$\frac{-(m-1)}{8}$=0,
∴m=1.
当m=1时,原方程为8x2-6=0,
解得:x1=$\frac{\sqrt{3}}{2}$,x2=-$\frac{\sqrt{3}}{2}$.
∴m为1时,方程的两个根互为相反数,这两个根分别为$\frac{\sqrt{3}}{2}$和-$\frac{\sqrt{3}}{2}$.
点评 本题考查了根与系数的关系、相反数以及一元二次方程的解,解题的关键是:(1)将x=0代入原方程求出m值;(2)根据相反数的定义结合根与系数的关系找出x1+x2=-$\frac{-(m-1)}{8}$=0.

练习册系列答案
相关题目
5.小伟掷一个质地均匀的正方体骰子,骰子的六个面上分别刻有1到6的点数.则向上的一面的点数小于3的概率为( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
 已知一次函数y=ax-c的图象如图所示,则二次函数y=ax2+c的图象大致是( )
已知一次函数y=ax-c的图象如图所示,则二次函数y=ax2+c的图象大致是( )



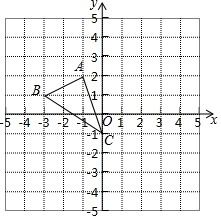 如图,在平面直角坐标系xOy中,已知A(-1,2),B(-3,1)C(0,-1)
如图,在平面直角坐标系xOy中,已知A(-1,2),B(-3,1)C(0,-1)