题目内容
5.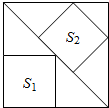 如图,边长为6的大正方形中有两个小正方形,若两个小正方形的面积分别为S1、S2,则S1+S2的值为17.
如图,边长为6的大正方形中有两个小正方形,若两个小正方形的面积分别为S1、S2,则S1+S2的值为17.
分析 由图可得,S2的边长为3,由AC=$\sqrt{2}$BC,BC=CE=$\sqrt{2}$CD,可得AC=2CD,CD=2,EC=2$\sqrt{2}$;然后,分别算出S1、S2的面积,即可解答.
解答 解:如图,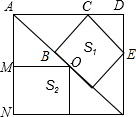
设正方形S1的边长为x,
∵△ABC和△CDE都为等腰直角三角形,
∴AB=BC,DE=DC,∠ABC=∠D=90°,
∴sin∠CAB=sin45°=$\frac{BC}{AC}$=$\frac{\sqrt{2}}{2}$即AC=$\sqrt{2}$BC,
同理可得:BC=CE=$\sqrt{2}$CD,
∴AC=$\sqrt{2}$BC=2CD,又AD=AC+CD=6,
∴CD=2,
∴EC2=22+22,即EC=2$\sqrt{2}$;
∴S1的面积为EC2=2$\sqrt{2}$×2$\sqrt{2}$=8;
∵∠MAO=∠MOA=45°,
∴AM=MO,
∵MO=MN,
∴AM=MN,
∴M为AN的中点,
∴S2的边长为3,
∴S2的面积为3×3=9,
∴S1+S2=8+9=17.
故答案为:17.
点评 本题考查了正方形的性质和等腰直角三角形的性质以及勾股定理的运用,同时也考查了学生的读图能力,熟记勾股定理是解题的关键.

练习册系列答案
相关题目
16.浙江省居民生活用电可申请峰谷电,峰谷电价如下表:
小远家5月份的高峰时间用电量为200千瓦时,低谷时间段用电量为300千瓦时,则按这种计费方式该家庭本月应付的电费为多少元?
| 高峰时间段用电价格表 | 低谷时间段用电价格表 | |
| 高峰电价 (单位:元/千瓦时) | 低谷月用电量 (单位:千瓦时) | 低谷电价 (单位:千瓦时) |
| 0.568 | 50及以下部分 | 0.288 |
| 超过50至200的部分 | 0.318 | |
| 超过200的部分 | 0.388 | |
20.关于函数y=$\frac{-{k}^{2}-2}{x}$,下列说法中错误的是( )
| A. | 当x>0时,y随x的增大而增大 | |
| B. | 当x<0时,y随x的增大而增大 | |
| C. | 当x=1时的函数值大于x=-1时的函数值 | |
| D. | 在函数图象所在的每个象限内,y都随x的增大而增大 |
10.已知M=x2+2xy,N=5x2-4xy,若M+N=4x2+P,则整式P为( )
| A. | 2x2-2xy | B. | 6x2-2xy | C. | 3x2+xy | D. | 2x2+xy |
17.下列各式结果为正数的是( )
| A. | -(-2) | B. | -(-2)2 | C. | -|-2| | D. | (-2)3 |
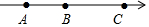 如图,已知数轴上A点表示数a,B点表示数b,C点表示数c.
如图,已知数轴上A点表示数a,B点表示数b,C点表示数c. 将如图所示的平面展开图折叠成正方体,则a对面的数字是-1.
将如图所示的平面展开图折叠成正方体,则a对面的数字是-1.