题目内容
15.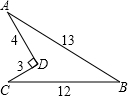 如图所示,某开发区有一块绿地ABCD,AD=3m,CD=4m,∠ADC=90°,CB=12,AB=13m,求这块绿地的面积.
如图所示,某开发区有一块绿地ABCD,AD=3m,CD=4m,∠ADC=90°,CB=12,AB=13m,求这块绿地的面积.
分析 连接AC,先根据勾股定理求出AC的长,再根据勾股定理的逆定理判断出△ACB的形状,根据S四边形ABC=S△ACB-S△ACD即可得出结论.
解答  解:连接AC,
解:连接AC,
∵AD=4,CD=3,∠ADC=90°,
∴AC=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∵AB=13,BC=12,
∴AC2+BC2=AB2,
∴△ACB是直角三角形,
∴S四边形ABC=S△ACB-S△ACD=$\frac{1}{2}$×5×12-$\frac{1}{2}$×3×4=30-6=24.
点评 本题考查的是勾股定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5.小伟掷一个质地均匀的正方体骰子,骰子的六个面上分别刻有1到6的点数.则向上的一面的点数小于3的概率为( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
16.浙江省居民生活用电可申请峰谷电,峰谷电价如下表:
小远家5月份的高峰时间用电量为200千瓦时,低谷时间段用电量为300千瓦时,则按这种计费方式该家庭本月应付的电费为多少元?
| 高峰时间段用电价格表 | 低谷时间段用电价格表 | |
| 高峰电价 (单位:元/千瓦时) | 低谷月用电量 (单位:千瓦时) | 低谷电价 (单位:千瓦时) |
| 0.568 | 50及以下部分 | 0.288 |
| 超过50至200的部分 | 0.318 | |
| 超过200的部分 | 0.388 | |