题目内容
关于x的二次函数y=x2+(2m-2)x-4m,以下结论:
①不论m取何值,抛物线交x轴有交点;
②不论m取何值,抛物线总经过点(-2,0);
③若m>0时,抛物线交x轴于A,点B两点,则AB>4;
④抛物线的顶点在y=-(x-2)2图象上.
其中正确的序号是 .
①不论m取何值,抛物线交x轴有交点;
②不论m取何值,抛物线总经过点(-2,0);
③若m>0时,抛物线交x轴于A,点B两点,则AB>4;
④抛物线的顶点在y=-(x-2)2图象上.
其中正确的序号是
考点:二次函数的性质
专题:
分析:①令y=0,得到关于x的一元二次方程,由判别式的正负可判断出与x轴是否有交点;
②可令x=-2,计算y是否为0;
③可令y=0,求得方程的两根,用m表示出AB,判断即可;
④可求得抛物线的顶点坐标,代入y=-(x-2)2看是否满足其解析式即可得出结论.
②可令x=-2,计算y是否为0;
③可令y=0,求得方程的两根,用m表示出AB,判断即可;
④可求得抛物线的顶点坐标,代入y=-(x-2)2看是否满足其解析式即可得出结论.
解答:解:①令y=0可得x2+(2m-2)x-4m=0,其判别式△=4(m-1)2+16m=4m2+8m+4=4(m+1)2≥0,所以无论m取何值,抛物线与x轴都有交点,故①正确;
②当x=-2时,代入可得y=(-2)2-2(2m-2)-4m=8-8m,只有当m=1时,才过(-2,0)点,所以②不正确;
③令y=0可得x2+(2m-2)x-4m=0,可解得x=2或x=-2m,由于m>0,所以AB=2-(-2m)=2+2m,只有当m>1时,AB>4,所以③不正确;
④可求得顶点坐标为(1-m,-(m+1)2),在y=-(x-2)2中,当x=1-m时,代入可得y=-(1-m-2)2=-(1-m)2,所以④正确;
故答案为:①④.
②当x=-2时,代入可得y=(-2)2-2(2m-2)-4m=8-8m,只有当m=1时,才过(-2,0)点,所以②不正确;
③令y=0可得x2+(2m-2)x-4m=0,可解得x=2或x=-2m,由于m>0,所以AB=2-(-2m)=2+2m,只有当m>1时,AB>4,所以③不正确;
④可求得顶点坐标为(1-m,-(m+1)2),在y=-(x-2)2中,当x=1-m时,代入可得y=-(1-m-2)2=-(1-m)2,所以④正确;
故答案为:①④.
点评:本题主要考查二次函数与x轴的交点及二次函数的顶点坐标,掌握一元二次方程与二次函数的关系是解题的关键.

练习册系列答案
相关题目
长度分别为3cm,5cm,7cm,9cm的四根木棒,能搭成(首尾连结)三角形的个数为( )
| A、1 | B、2 | C、3 | D、4 |
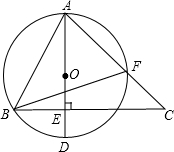 如图,AD是⊙O的直径,AB、AF是弦,BE⊥AD与AF的延长线交于点C.
如图,AD是⊙O的直径,AB、AF是弦,BE⊥AD与AF的延长线交于点C.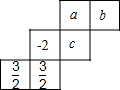 如图,是一个正方体纸盒的表面展开图,在其中的三个正方形a,b,c 内分别填入适当的数,使得折成正方体后相对的面上的两个数满足下列条件:
如图,是一个正方体纸盒的表面展开图,在其中的三个正方形a,b,c 内分别填入适当的数,使得折成正方体后相对的面上的两个数满足下列条件: 如图,等边△OAB和等边△AFE的一边都在x轴上,双曲线y=
如图,等边△OAB和等边△AFE的一边都在x轴上,双曲线y=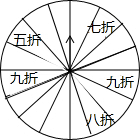 某酒店为了吸引顾客,设立了一个可以自由转动的转盘(如图,转盘等分成16份),并规定:顾客消费100元以上(不包括100元),就能获得一次转动转盘的机会;如果转盘停止后,指针正好对准九折、八折、七折或五折区域,顾客就可以获得此项待遇.
某酒店为了吸引顾客,设立了一个可以自由转动的转盘(如图,转盘等分成16份),并规定:顾客消费100元以上(不包括100元),就能获得一次转动转盘的机会;如果转盘停止后,指针正好对准九折、八折、七折或五折区域,顾客就可以获得此项待遇.