题目内容
长度分别为3cm，5cm，7cm，9cm的四根木棒，能搭成（首尾连结）三角形的个数为（ ）
| A、1 | B、2 | C、3 | D、4 |
考点：三角形三边关系
专题：
分析：首先能够找到所有的情况，然后根据三角形的三边关系“任意两边之和大于第三边，任意两边之差小于第三边”，进行分析．
解答：解：根据三角形的三边关系，得3，5，7；3，7，9；5，7，9都能组成三角形．
故有3个．
故选C．
故有3个．
故选C．
点评：本题考查了三角形三边关系定理：三角形两边之和大于第三边．在运用三角形三边关系判定三条线段能否构成三角形时并不一定要列出三个不等式，只要两条较短的线段长度之和大于第三条线段的长度即可判定这三条线段能构成一个三角形．
练习册系列答案
相关题目
如图，在△ABC中，D是AB边上的点，以点D为顶点作∠ADE，使∠ADE=∠C，DE交边A C于点E．若AB=8，AC=6，AD=3，则AE=
如图，在△ABC中，AB=AC，D为BC中点，四边形ABDE是平行四边形，AC，DE相交于点O．
如图，在长方形ABCD中，E是AD的中点，F是CE的中点．若△BDF的面积是5平方厘米，则长方形ABCD的面积是
如图，△ABC≌△DEF，BE=1.3，AE=1，则DE的长是（ ）| A、0.3 | B、1 |
| C、1.3 | D、2.3 |
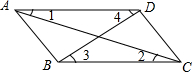如图，下列四组条件中能说明AB∥CD的是（ ）| A、∠ABC=∠ADC，∠3=∠4 |
| B、∠1=∠2 |
| C、∠BAD+∠ABC=180° |
| D、∠BAD=∠BCD |