题目内容
12. 如图,用一块直径为a的圆桌布平铺在对角线长为a的正方形桌面上,若四周下垂的最大长度相等,则桌布下垂的最大长度x为( )
如图,用一块直径为a的圆桌布平铺在对角线长为a的正方形桌面上,若四周下垂的最大长度相等,则桌布下垂的最大长度x为( )| A. | $\frac{{2-\sqrt{2}}}{4}a$ | B. | $\frac{{\sqrt{2}-1}}{2}a$ | C. | $({\sqrt{2}-1})a$ | D. | $({2-\sqrt{2}})a$ |
分析 如图,正方形ABCD为直径为a的⊙O的内接正方形,作OE⊥BC于E,交⊙O于F,连接OB,则OB=$\frac{1}{2}$a,则可判断△OBE为等腰直角三角形,所以OE=$\frac{\sqrt{2}}{2}$OB=$\frac{\sqrt{2}}{4}$a,然后计算OF-OE即可.
解答 解:如图,正方形ABCD为直径为a的⊙O的内接正方形,作OE⊥BC于E,交⊙O于F,连接OB,则OB=$\frac{1}{2}$a,
∴△OBE为等腰直角三角形,
∴OE=$\frac{\sqrt{2}}{2}$OB=$\frac{\sqrt{2}}{4}$a,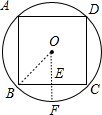
∴EF=OF-OE=$\frac{1}{2}$a-$\frac{\sqrt{2}}{4}$a=$\frac{2-\sqrt{2}}{4}$a.
即桌布下垂的最大长度x为$\frac{2-\sqrt{2}}{4}$a.
故选A.
点评 本题考查了垂径定理的应用:垂径定理和勾股定理相结合,构造直角三角形,可解决计算弦长、半径、弦心距等问题.也考查了正方形的性质.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
3.一个钟表时针长6厘米,从7时到11时,时针针尖走了( )
| A. | 6π厘米 | B. | 2π厘米 | C. | 4π厘米 | D. | 12π厘米 |
20.在下列四边形中,对角线交点到各顶点的距离一定相等的四边形是( )
| A. | 四边形 | B. | 平行四边形 | C. | 矩形 | D. | 菱形 |
7. 如图,在△ABC中,BC边上的高是( )
如图,在△ABC中,BC边上的高是( )
 如图,在△ABC中,BC边上的高是( )
如图,在△ABC中,BC边上的高是( )| A. | CE | B. | AD | C. | CF | D. | AB |
17.如果教室“第5组第2个”同学的座位用(5,2)表示,那么“第2组第3个”同学的座位可以表示成( )
| A. | (2,3) | B. | (3,2) | C. | (3,3) | D. | (2,2) |
1.设▲,●,■表示三种不同的物体,现用天平称了两次,情况如图所示,那么▲,●,■这三种物体的质量从大到小的顺序排列应为( )


| A. | ▲,●,■ | B. | ▲,■,● | C. | ■,●,▲ | D. | ●,▲,■ |
2.若A=x2+4xy+y2-4,B=4x+4xy-6y-25,则A、B的大小关系为( )
| A. | A>B | B. | A<B | C. | A=B | D. | 无法确定 |