题目内容
7.(1)解不等式组:-2$<1-\frac{1}{2}x≤3$(2)化简:$\frac{2a}{{a}^{2}-4}•(\frac{{a}^{2}+4}{4a}-1)$.
分析 (1)求出每个不等式的解集,根据找不等式组解集的规律找出即可;
(2)首先把括号里的式子进行通分,然后进行因式分解,再约分化简即可求解.
解答 解:(1)原不等式组化为$\left\{\begin{array}{l}{-2<1-\frac{1}{2}x①}\\{1-\frac{1}{2}x≤3②}\end{array}\right.$,
解不等式①得:x<6,
解不等式②得:x≥-4,
故不等式组的解集是-4≤x<6;
(2)$\frac{2a}{{a}^{2}-4}•(\frac{{a}^{2}+4}{4a}-1)$
=$\frac{2a}{(a+2)(a-2)}$•$\frac{{a}^{2}+4-4a}{4a}$
=$\frac{2a}{(a+2)(a-2)}$•$\frac{(a-2)^{2}}{4a}$
=$\frac{a-2}{2(a+2)}$.
点评 本题考查了解一元一次不等式和解一元一次不等式组的应用,解题的关键是能根据不等式的解集找出不等式组的解集.同时考查分式的混合运算,通分、因式分解和约分是解答的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.“三次投掷一枚硬币,三次正面朝上”这一事件是( )
| A. | 必然事件 | B. | 随机事件 | C. | 确定事件 | D. | 不可能事件 |
17. 如图,四边形ABCD是轴对称图形,直线AC是它的对称轴,若∠BAD=150°,∠B=40°,则∠BCD的大小为( )
如图,四边形ABCD是轴对称图形,直线AC是它的对称轴,若∠BAD=150°,∠B=40°,则∠BCD的大小为( )
 如图,四边形ABCD是轴对称图形,直线AC是它的对称轴,若∠BAD=150°,∠B=40°,则∠BCD的大小为( )
如图,四边形ABCD是轴对称图形,直线AC是它的对称轴,若∠BAD=150°,∠B=40°,则∠BCD的大小为( )| A. | 150° | B. | 140° | C. | 130° | D. | 120° |
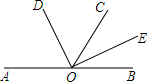 如图,已知A、O、B三点在同一条直线上,OD平分∠AOC,OE平分∠BOC.若∠BOC=62°,求∠DOE的度数.
如图,已知A、O、B三点在同一条直线上,OD平分∠AOC,OE平分∠BOC.若∠BOC=62°,求∠DOE的度数. 如图,已知,在△ABC中,BA=BC=20cm,AC=30cm,点P从A点出发,沿AB以4cm/s的速度向点B运动;同时点Q从C点出发,沿CA以每秒3cm的速度向A点运动,设运动时间为x秒.
如图,已知,在△ABC中,BA=BC=20cm,AC=30cm,点P从A点出发,沿AB以4cm/s的速度向点B运动;同时点Q从C点出发,沿CA以每秒3cm的速度向A点运动,设运动时间为x秒.

 如图,已知反比例函数y=$\frac{k}{x}$(k≠0)的图象过点A(-3,2).
如图,已知反比例函数y=$\frac{k}{x}$(k≠0)的图象过点A(-3,2).