题目内容
15. 如图,已知,在△ABC中,BA=BC=20cm,AC=30cm,点P从A点出发,沿AB以4cm/s的速度向点B运动;同时点Q从C点出发,沿CA以每秒3cm的速度向A点运动,设运动时间为x秒.
如图,已知,在△ABC中,BA=BC=20cm,AC=30cm,点P从A点出发,沿AB以4cm/s的速度向点B运动;同时点Q从C点出发,沿CA以每秒3cm的速度向A点运动,设运动时间为x秒.(1)当x为何值时,PQ∥BC;
(2)S△BCQ:S△ABC=1:3时,求S△BPQ:S△ABC的值;
(3)在现有条件下,哪些边对应成比例就能使△APQ与△CQB相似?并写出对应成比例的边.
分析 (1)当PQ∥BC时,根据平行线分线段成比例定理,可得出关于AP,PQ,AB,AC的比例关系式,我们可根据P,Q的速度,用时间x表示出AP,AQ,然后根据得出的关系式求出x的值.
(2)由三角形的面积关系得出CQ:AC=1:3,那么CQ=10cm,此时时间x正好是(1)的结果,那么此时PQ∥BC,由此可根据平行这个特殊条件,得出三角形APQ和ABC的面积比,然后再根据三角形PBQ的面积=三角形ABC的面积-三角形APQ的面积-三角形BQC的面积来得出三角形BPQ和三角形ABC的面积比.
(3)分两种情况进行讨论.由等腰三角形的性质得出∠A和∠C对应相等,那么就要分成AP和CQ对应成比例以及AP和BC对应成比例两种情况.
解答 解:(1)当PQ∥BC时,AP:AB=AQ:AC,
∵AP=4x,AQ=30-3x,
∴$\frac{4x}{20}$=$\frac{30-2x}{30}$,
解得:x=$\frac{10}{3}$;
即当x=$\frac{10}{3}$,PQ∥BC;
(2)∵S△BCQ:S△ABC=1:3
∴CQ:AC=1:3,
∴CQ=10c,
∴时间用了$\frac{10}{3}$秒,
∴AP=$\frac{40}{3}$cm,
∵由(1)知,此时PQ∥BC,
∴△APQ∽△ABC,相似比为$\frac{2}{3}$,
∴S△APQ:S△ABC=4:9,
∴四边形PQCB与三角形ABC面积比为5:9,即S四边形PQCB=,$\frac{5}{9}$S△ABC,
又∵S△BCQ:S△ABC=1:3,即S△BCQ=$\frac{1}{3}$S△ABC,
∴S△BPQ=S四边形PQCB-S△BCQ═$\frac{5}{9}$S△ABC-$\frac{1}{3}$S△ABC=$\frac{2}{9}$S△ABC,
∴S△BPQ:S△ABC=2:9=$\frac{2}{9}$;
(3)∵BA=BC,
∴∠A=∠C,
当AP:CQ=AQ:BC,△APQ∽△CQB;
当AQ:CQ=AP:BC,△APQ∽△CBQ;
∴对应成比例的边为$\frac{AP}{CQ}=\frac{AQ}{BC}$或$\frac{AQ}{CQ}=\frac{AP}{BC}$.
点评 本题是相似形综合题目,主要考查了相似三角形的判定和性质、平行线分线段成比例定理;根据三角形相似得出线段比或面积比是解题的关键.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案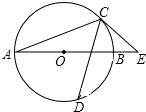 如图,AB是⊙O的直径,C,D是⊙O上两点,连接AD,CD,AD=CD,过点C作⊙O的切线交AB的延长线于点E,若∠E=50°,则∠DAC等于( )
如图,AB是⊙O的直径,C,D是⊙O上两点,连接AD,CD,AD=CD,过点C作⊙O的切线交AB的延长线于点E,若∠E=50°,则∠DAC等于( )| A. | 40° | B. | 50° | C. | 55° | D. | 60° |
 如图:AB∥DE,∠B=30°,∠C=110°,∠D的度数为( )
如图:AB∥DE,∠B=30°,∠C=110°,∠D的度数为( )| A. | 115° | B. | 120° | C. | 100° | D. | 80° |