题目内容
19.PA切⊙O于点P,AB交⊙O于C、B两点.(1)如图1,求证:∠APC=∠ABP;
(2)如图2,M是⊙O内一点,AM交⊙O于点N,若PA=6,MN=NA=3,OM=2,求⊙O半径的长.

分析 (1)连接OP,根据切线的性质和圆周角定理得出∠OPA=∠BPC=90°,即可证得∠OPB=∠APC,根据等边对等角证得∠ABP=∠OPB,即可证得∠APC=∠ABP;
(2)延长AM,交⊙O于点H,作直线OM,交⊙O于两点E、F,由PA2=AN•AH,求得AH=12,即可得出MH=AH-AM=6,设⊙O的半径为r,则EM=r+2,FM=r-2,根据相交弦定理得出(r+2)(r-2)=6×3,即可求得半径.
解答 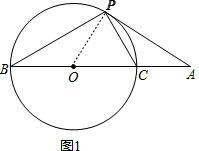 (1)证明:连接OP,
(1)证明:连接OP,
∵PA切⊙O于点P,
∴OP⊥PA,
∴∠APC+∠OPC=90°,
∵BC是直径,
∴∠BPC=90°,
∴∠OPB+∠OPC=90°,
∴∠OPB=∠APC,
∵OP=OB,
∴∠ABP=∠OPB,
∴∠APC=∠ABP;
(2)解:延长AM,交⊙O于点H,作直线OM,交⊙O于两点E、F,
∵PA切⊙O于点P,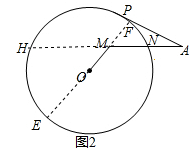
∴PA2=AN•AH,即62=3AH,
∴AH=12,
∴MH=AH-AM=12-3-3=6,
设⊙O的半径为r,则EM=r+2,FM=r-2,
∵EM•FM=HM•MN,
∴(r+2)(r-2)=6×3,
解得r=$\sqrt{22}$.
点评 本题考查了切线的性质以及相交弦定理,作出辅助线创造应用相交弦定理的条件是解题的关键.

练习册系列答案
 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
14. 四边形ABCD中,已知∠B=80°,∠C=60°,AP、DP分别平分∠BAD、∠ADC,则∠P的度数是( )
四边形ABCD中,已知∠B=80°,∠C=60°,AP、DP分别平分∠BAD、∠ADC,则∠P的度数是( )
 四边形ABCD中,已知∠B=80°,∠C=60°,AP、DP分别平分∠BAD、∠ADC,则∠P的度数是( )
四边形ABCD中,已知∠B=80°,∠C=60°,AP、DP分别平分∠BAD、∠ADC,则∠P的度数是( )| A. | 60° | B. | 70° | C. | 80° | D. | 90° |
 已知:平面直角坐标系xOy中,直线y=kx+b(k≠0)与直线y=mx(m≠0)交于点A(-2,4).
已知:平面直角坐标系xOy中,直线y=kx+b(k≠0)与直线y=mx(m≠0)交于点A(-2,4). 为了了解某校全体学生参加消防知识竞赛的成绩(均为整数),从中抽取了10%的学生竞赛成绩,整理后绘制如下的频数分布直方图,其中,每组可含量最低值,不含最高值.
为了了解某校全体学生参加消防知识竞赛的成绩(均为整数),从中抽取了10%的学生竞赛成绩,整理后绘制如下的频数分布直方图,其中,每组可含量最低值,不含最高值.