题目内容
18.在Rt△ABC中,∠C=90°,AC=2,BC=1,则sinA=$\frac{\sqrt{5}}{5}$.分析 根据勾股定理求出AB,根据正弦的定义计算即可.
解答 解:∵∠C=90°,AC=2,BC=1,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{5}$,
∴sinA=$\frac{BC}{AB}$=$\frac{\sqrt{5}}{5}$.
故答案为:$\frac{\sqrt{5}}{5}$.
点评 本题考查的是锐角三角函数的定义,在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边.

练习册系列答案
相关题目
3.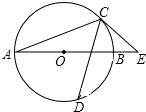 如图,AB是⊙O的直径,C,D是⊙O上两点,连接AD,CD,AD=CD,过点C作⊙O的切线交AB的延长线于点E,若∠E=50°,则∠DAC等于( )
如图,AB是⊙O的直径,C,D是⊙O上两点,连接AD,CD,AD=CD,过点C作⊙O的切线交AB的延长线于点E,若∠E=50°,则∠DAC等于( )
 如图,AB是⊙O的直径,C,D是⊙O上两点,连接AD,CD,AD=CD,过点C作⊙O的切线交AB的延长线于点E,若∠E=50°,则∠DAC等于( )
如图,AB是⊙O的直径,C,D是⊙O上两点,连接AD,CD,AD=CD,过点C作⊙O的切线交AB的延长线于点E,若∠E=50°,则∠DAC等于( )| A. | 40° | B. | 50° | C. | 55° | D. | 60° |
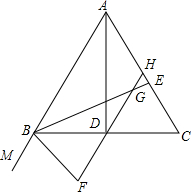 已知,在△ABC中,AB=AC,AD、BE分别是△ABC的角平分线,H为AC的中点,连接HD,交BE于G,BF平分∠MBC,交HD的延长线于F.
已知,在△ABC中,AB=AC,AD、BE分别是△ABC的角平分线,H为AC的中点,连接HD,交BE于G,BF平分∠MBC,交HD的延长线于F.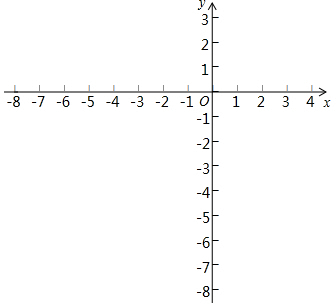 已知:平面直角坐标系xOy中,直线y=kx+b(k≠0)与直线y=mx(m≠0)交于点A(-2,4).
已知:平面直角坐标系xOy中,直线y=kx+b(k≠0)与直线y=mx(m≠0)交于点A(-2,4).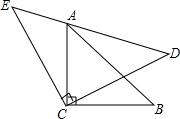 如图,在等腰直角三角形Rt△ABC和Rt△ECD中,Rt△ACB的顶点A在Rt△ECD的斜边ED上,求证:AE2+AD2=2AC2.(提示:添加辅助线连接BD)
如图,在等腰直角三角形Rt△ABC和Rt△ECD中,Rt△ACB的顶点A在Rt△ECD的斜边ED上,求证:AE2+AD2=2AC2.(提示:添加辅助线连接BD)