题目内容
11.计算:${2^{-2}}+{(\sqrt{3})^0}-|{-2}|$=$-\frac{3}{4}$.分析 根据实数的运算顺序,首先计算乘方,然后从左向右依次计算,求出算式${2^{-2}}+{(\sqrt{3})^0}-|{-2}|$的值是多少即可.
解答 解:${2^{-2}}+{(\sqrt{3})^0}-|{-2}|$
=$\frac{1}{4}$+1-2
=1$\frac{1}{4}$-2
=-$\frac{3}{4}$
故答案为:-$\frac{3}{4}$.
点评 (1)此题主要考查了实数的运算,要熟练掌握,解答此题的关键是要明确:在进行实数运算时,和有理数运算一样,要从高级到低级,即先算乘方、开方,再算乘除,最后算加减,有括号的要先算括号里面的,同级运算要按照从左到右的顺序进行.另外,有理数的运算律在实数范围内仍然适用.
(2)此题还考查了零指数幂的运算,要熟练掌握,解答此题的关键是要明确:①a0=1(a≠0);②00≠1.
(3)此题还考查了负整数指数幂的运算,要熟练掌握,解答此题的关键是要明确:①a-p=$\frac{1}{{a}^{p}}$(a≠0,p为正整数);②计算负整数指数幂时,一定要根据负整数指数幂的意义计算;③当底数是分数时,只要把分子、分母颠倒,负指数就可变为正指数.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
1.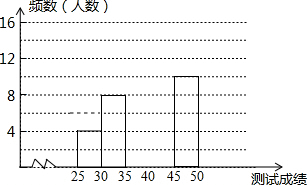 某校九年级举办了首届“汉字听写大赛”,全校500名九年级学生全部参加,他们同时听写50个汉字,每正确听写出一个汉字得1分,为了解学生们的成绩,随机抽取了部分学生的成绩,并根据测试成绩绘制出如下两幅不完整的统计表和频数分布直方图:
某校九年级举办了首届“汉字听写大赛”,全校500名九年级学生全部参加,他们同时听写50个汉字,每正确听写出一个汉字得1分,为了解学生们的成绩,随机抽取了部分学生的成绩,并根据测试成绩绘制出如下两幅不完整的统计表和频数分布直方图:
(1)求此次抽查了多少名学生的成绩;
(2)通过计算将频数分布直方图补充完整;
(3)若测试成绩不低于40分为优秀,请估计本次测试九年级学生中成绩优秀的人数.
 某校九年级举办了首届“汉字听写大赛”,全校500名九年级学生全部参加,他们同时听写50个汉字,每正确听写出一个汉字得1分,为了解学生们的成绩,随机抽取了部分学生的成绩,并根据测试成绩绘制出如下两幅不完整的统计表和频数分布直方图:
某校九年级举办了首届“汉字听写大赛”,全校500名九年级学生全部参加,他们同时听写50个汉字,每正确听写出一个汉字得1分,为了解学生们的成绩,随机抽取了部分学生的成绩,并根据测试成绩绘制出如下两幅不完整的统计表和频数分布直方图:| 组别 | 成绩x分 | 人数 | 频率 |
| 1组 | 25≤<30 | 4 | 0.08 |
| 2组 | 30≤x<35 | 8 | 0.16 |
| 3组 | 35≤x<40 | a | 0.32 |
| 4组 | 40≤x<45 | b | c |
| 5组 | 45≤x<50 | 10 | 0.2 |
(2)通过计算将频数分布直方图补充完整;
(3)若测试成绩不低于40分为优秀,请估计本次测试九年级学生中成绩优秀的人数.
2.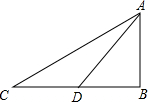 如图,从地面上C、D两处望山顶A,仰角分别为30°和45°,若C、D两处相距200米,则山高AB为( )
如图,从地面上C、D两处望山顶A,仰角分别为30°和45°,若C、D两处相距200米,则山高AB为( )
 如图,从地面上C、D两处望山顶A,仰角分别为30°和45°,若C、D两处相距200米,则山高AB为( )
如图,从地面上C、D两处望山顶A,仰角分别为30°和45°,若C、D两处相距200米,则山高AB为( )| A. | 100($\sqrt{3}$+1)米 | B. | 100米 | C. | 100$\sqrt{2}$ | D. | 200$\sqrt{3}$ |
1.2016年1月19日,国家统计局公布了2015年宏观经济数据,初步核算,全年国内生产总值为676000亿元.676000用科学记数法表示为( )
| A. | 6.76×106 | B. | 6.76×105 | C. | 67.6×105 | D. | 0.676×106 |
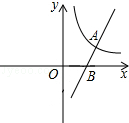 如图,直线y=2x-6与反比例函数y=$\frac{k}{x}$(k>0)的图象交于点A(4,2),与x轴交于点B.
如图,直线y=2x-6与反比例函数y=$\frac{k}{x}$(k>0)的图象交于点A(4,2),与x轴交于点B.