题目内容
13.(1)化简:$\sqrt{12}$+$\sqrt{27}$+$\frac{1}{4}$$\sqrt{48}$-15$\sqrt{\frac{1}{3}}$(2)计算:(3+$\sqrt{5}$)2-2$\sqrt{5}$.
分析 (1)各项化为最简后,合并同类二次根式即可得到结果;
(2)先根据乘法公式计算出(3+$\sqrt{5}$)2的值,然后合并同类二次根式即可.
解答 (1)解:$\sqrt{12}$+$\sqrt{27}$+$\frac{1}{4}$$\sqrt{48}$-15$\sqrt{\frac{1}{3}}$
=2$\sqrt{3}$+3$\sqrt{3}$+$\sqrt{3}$-5$\sqrt{3}$
=$\sqrt{3}$
(2)解:(3+$\sqrt{5}$)2-2$\sqrt{5}$
=9+6$\sqrt{5}$+5-2$\sqrt{5}$
=14+4$\sqrt{5}$.
点评 此题考查了二次根式的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.某煤矿原计划x天生存120t煤,由于采用新的技术,每天增加生存3t,因此提前2天完成,列出的方程为( )
| A. | $\frac{120}{x-2}$=$\frac{120}{x}$=-3 | B. | $\frac{120}{x}=\frac{120}{x+2}$-3 | C. | $\frac{120}{x+2}=\frac{120}{x}$-3 | D. | $\frac{120}{x}$=$\frac{120}{x-2}$-3 |
18.下列计算正确的是( )
| A. | a2+a3=a5 | B. | a2•a3=a6 | C. | (a2)3=a6 | D. | ($\frac{a}{2}$)2=$\frac{{a}^{2}}{2}$ |
5.已知:(a-b)2=9;(a+b)2=25,则a2+b2=( )
| A. | 34 | B. | 16 | C. | -16 | D. | 17 |
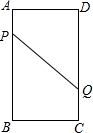 A、B、C、D为矩形的4个顶点,AB=16cm,BC=6cm,动点P、Q分别从A、C同时出发,点P以3厘米每秒的速度向点B移动,一直到达点B为止,点Q以2厘米每秒的速度向点D移动.
A、B、C、D为矩形的4个顶点,AB=16cm,BC=6cm,动点P、Q分别从A、C同时出发,点P以3厘米每秒的速度向点B移动,一直到达点B为止,点Q以2厘米每秒的速度向点D移动. 实数a、b在数轴上的位置如图所示,则化简 $\sqrt{{{(-a)}^2}}+\sqrt{b^2}-\sqrt{{{(a+b)}^2}}$的结果为2b.
实数a、b在数轴上的位置如图所示,则化简 $\sqrt{{{(-a)}^2}}+\sqrt{b^2}-\sqrt{{{(a+b)}^2}}$的结果为2b.