题目内容
3.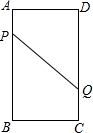 A、B、C、D为矩形的4个顶点,AB=16cm,BC=6cm,动点P、Q分别从A、C同时出发,点P以3厘米每秒的速度向点B移动,一直到达点B为止,点Q以2厘米每秒的速度向点D移动.
A、B、C、D为矩形的4个顶点,AB=16cm,BC=6cm,动点P、Q分别从A、C同时出发,点P以3厘米每秒的速度向点B移动,一直到达点B为止,点Q以2厘米每秒的速度向点D移动.(1)经过多长时间P、Q两点之间的距离是10cm?
(2)经过多长时间,四边形APQD是矩形?
(3)P、Q两点从出发开始几秒时,在AB上存在一点M,使△PMQ为等边三角形.
分析 (1)作PH⊥CD,垂足为H,设运动时间为t秒,用t表示线段长,用勾股定理列方程求解;
(2)根据矩形的性质得出AP=DQ,即可求出t的值;
(3)根据等边三角形的性质得出PQ=PM,根据勾股定理得出关于t的方程,求出方程的解即可.
解答 解:(1)设P,Q两点从出发经过t秒时,点P,Q间的距离是10cm,
作PH⊥CD,垂足为H,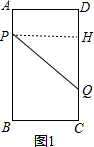
则PH=AD=6,PQ=10,HQ=CD-AP-CQ=16-5t,
∵PH2+HQ2=PQ2
可得:(16-5t)2+62=102,
解得t1=4.8,t2=1.6.
答:P,Q两点从出发经过1.6或4.8秒时,点P,Q间的距离是10cm
(2)要使APQD是矩形,必须AP=DQ,
即3t=16-2t,
解得:t=$\frac{16}{5}$,
即经过$\frac{16}{5}$s时,四边形APQD是矩形;
(3)如图2,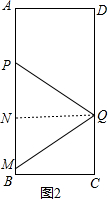
过Q作QN⊥AB于N,
∵△PQM是等边三角形,
∴PQ=PM,
∵AP=3t,CQ=BN=2t,
∴PN=MN=16-3t-2t=16-5t,
∵PQ=PM,
∴PQ2=PM2,
∴62+(16-5t)2=(16-5t+16-5t)2,
解得:t=$\frac{16±2\sqrt{3}}{5}$,
所以P、Q两点从出发开始$\frac{16±2\sqrt{3}}{5}$秒时,在AB上存在一点M,使△PMQ为等边三角形.
点评 此题考查了矩形的性质,勾股定理,等边三角形的性质,一元二次方程的运用,利用作垂线,构造直角三角形,运用勾股定理列方程是解题关键.

练习册系列答案
相关题目
12.下列运算,正确的是( )
| A. | 4a-2a=2 | B. | a6÷a3=a2 | C. | (a-b)2=a2-b2 | D. | (-a3b)2=a6b2 |
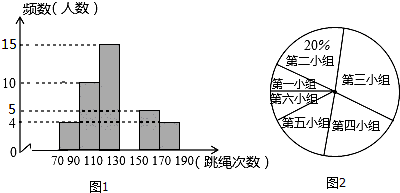
 为响应李克强总理的“全民阅读”号召,某数学兴趣小组随机调查了该校40名学生平均每天的阅读时间,统计结果如图所示.如果该校有1200名学生,则每天阅读时间不少于1.5小时的学生大约有390人.
为响应李克强总理的“全民阅读”号召,某数学兴趣小组随机调查了该校40名学生平均每天的阅读时间,统计结果如图所示.如果该校有1200名学生,则每天阅读时间不少于1.5小时的学生大约有390人.