题目内容
1.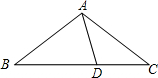 如图,在△ABC中,AB=AC,D为BC上一点,且DA=DC,BD=BA,则∠B的大小为( )
如图,在△ABC中,AB=AC,D为BC上一点,且DA=DC,BD=BA,则∠B的大小为( )| A. | 40° | B. | 36° | C. | 30° | D. | 25° |
分析 根据AB=AC可得∠B=∠C,CD=DA可得∠ADB=2∠C=2∠B,BA=BD,可得∠BDA=∠BAD=2∠B,在△ABD中利用三角形内角和定理可求出∠B.
解答 解:∵AB=AC,
∴∠B=∠C,
∵CD=DA,
∴∠C=∠DAC,
∵BA=BD,
∴∠BDA=∠BAD=2∠C=2∠B,
又∵∠B+∠BAD+∠BDA=180°,
∴5∠B=180°,
∴∠B=36°,
故选B.
点评 本题主要考查等腰三角形的性质,掌握等边对等角是解题的关键,注意三角形内角和定理和方程思想的应用.

练习册系列答案
相关题目
12.下列关于一次函数y=-2x+1的说法,其中正确的是( )
| A. | 图象经过第一、二、三象限 | B. | 图象经过点(-2,1) | ||
| C. | 当x>1时,y<0 | D. | y随x的增大而增大 |
16. 如图,直线AC∥BD,AO、BO分别是∠BAC、∠ABD的平分线,那么下列结论错误的是( )
如图,直线AC∥BD,AO、BO分别是∠BAC、∠ABD的平分线,那么下列结论错误的是( )
 如图,直线AC∥BD,AO、BO分别是∠BAC、∠ABD的平分线,那么下列结论错误的是( )
如图,直线AC∥BD,AO、BO分别是∠BAC、∠ABD的平分线,那么下列结论错误的是( )| A. | ∠BAO与∠CAO相等 | B. | ∠BAC与∠ABD互补 | C. | ∠BAO与∠ABO互余 | D. | ∠ABO与∠DBO不等 |
9.下列说法错误的是( )
| A. | 一组对边平行且另一组对边相等的四边形是平行四边形 | |
| B. | 两组对角都相等的四边形是平行四边形 | |
| C. | 一组对边平行且一组对角相等的四边形是平行四边形 | |
| D. | 一组对边平行,一组邻角互补的四边形是平行四边形 |
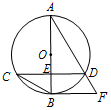 如图,已知⊙O的直径AB与弦CD互相垂直,垂足为点E.⊙O的切线BF与弦AD的延长线相交于点F,且AF=5,cos∠BCD=$\frac{3}{4}$.
如图,已知⊙O的直径AB与弦CD互相垂直,垂足为点E.⊙O的切线BF与弦AD的延长线相交于点F,且AF=5,cos∠BCD=$\frac{3}{4}$.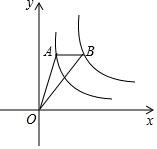 如图,点A是反比例函数y1=$\frac{{k}_{1}}{x}$(x>0)图象上一点,过点A作x轴的平行线,交反比例函数y2=$\frac{{k}_{2}}{x}$(x>0)的图象于点B,连接OA,OB,若△OAB的面积为2,则k2-k1的值为( )
如图,点A是反比例函数y1=$\frac{{k}_{1}}{x}$(x>0)图象上一点,过点A作x轴的平行线,交反比例函数y2=$\frac{{k}_{2}}{x}$(x>0)的图象于点B,连接OA,OB,若△OAB的面积为2,则k2-k1的值为( ) 如图,直线y=kx+b(k、b为常数)分别与x轴、y轴交于点A(-4,0)、B(0,3),抛物线y=-x2+2x+1与y轴交于点C.
如图,直线y=kx+b(k、b为常数)分别与x轴、y轴交于点A(-4,0)、B(0,3),抛物线y=-x2+2x+1与y轴交于点C.