题目内容
9.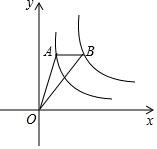 如图,点A是反比例函数y1=$\frac{{k}_{1}}{x}$(x>0)图象上一点,过点A作x轴的平行线,交反比例函数y2=$\frac{{k}_{2}}{x}$(x>0)的图象于点B,连接OA,OB,若△OAB的面积为2,则k2-k1的值为( )
如图,点A是反比例函数y1=$\frac{{k}_{1}}{x}$(x>0)图象上一点,过点A作x轴的平行线,交反比例函数y2=$\frac{{k}_{2}}{x}$(x>0)的图象于点B,连接OA,OB,若△OAB的面积为2,则k2-k1的值为( )| A. | -2 | B. | 2 | C. | -4 | D. | 4 |
分析 延长BA交y轴于点D,由反比例函数系数k的几何意义即可得出S△AOD=$\frac{1}{2}$k1,S△OBD=$\frac{1}{2}$k2,再根据S△OAB=S△BOD-S△AOD=2即可求出k值.
解答 解:延长BA交y轴于点D,如图所示.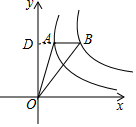
∵点A、B是函数y=$\frac{{k}_{1}}{x}$(x>0)和y=$\frac{{k}_{2}}{x}$(x>0)图象上一点,
∴S△AOD=$\frac{1}{2}$k1,S△OBD=$\frac{1}{2}$k2,
∴S△OAB=S△BOD-S△AOD=2.
∴$\frac{1}{2}$k2-$\frac{1}{2}$k1=2,
则k2-k1=4.
故选D.
点评 本题考查了反比例函数系数k的几何意义,通过面积间的关系是解题的关键.

练习册系列答案
相关题目
19.已知点A(a,1)与点A′(5,b)关于y轴对称,则实数a、b的值是( )
| A. | a=5,b=1 | B. | a=-5,b=1 | C. | a=5,b=-1 | D. | a=-5,b=-1 |
17.已知关于x的方程x2+2x+k=0没有实数根,则k的取值范围是( )
| A. | k<1 | B. | k>1 | C. | k<-1 | D. | k>-1 |
4.2016年12月28日,南宁地铁1号线全线开通运营,1号线西起石埠站,冬至南宁东站,全线长32100米,其中数据32100用科学记数法表示为( )
| A. | 0.321×105 | B. | 3.21×104 | C. | 32.1×103 | D. | 321×102 |
14.计算-(-1)+|-1|,其结果为( )
| A. | -2 | B. | 2 | C. | 0 | D. | -1 |
1.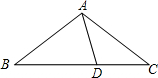 如图,在△ABC中,AB=AC,D为BC上一点,且DA=DC,BD=BA,则∠B的大小为( )
如图,在△ABC中,AB=AC,D为BC上一点,且DA=DC,BD=BA,则∠B的大小为( )
 如图,在△ABC中,AB=AC,D为BC上一点,且DA=DC,BD=BA,则∠B的大小为( )
如图,在△ABC中,AB=AC,D为BC上一点,且DA=DC,BD=BA,则∠B的大小为( )| A. | 40° | B. | 36° | C. | 30° | D. | 25° |