题目内容
11.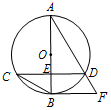 如图,已知⊙O的直径AB与弦CD互相垂直,垂足为点E.⊙O的切线BF与弦AD的延长线相交于点F,且AF=5,cos∠BCD=$\frac{3}{4}$.
如图,已知⊙O的直径AB与弦CD互相垂直,垂足为点E.⊙O的切线BF与弦AD的延长线相交于点F,且AF=5,cos∠BCD=$\frac{3}{4}$.(1)求⊙O的半径;
(2)求弦CD的长.
分析 (1)由切线性质知∠ABF=90°,根据∠BCD=∠BAD知cos∠BCD=cos∠BAF=$\frac{AB}{AF}$=$\frac{3}{4}$,可得AB=$\frac{3}{4}$AF=$\frac{15}{4}$,从而得出答案;
(2)连结BD,解直角三角形分别得到AD=ABcos∠BAD=$\frac{45}{16}$、BF=$\frac{5\sqrt{7}}{4}$、sin∠BAF=$\frac{BF}{AF}$=$\frac{\sqrt{7}}{4}$,由ED=ADsin∠EAD可得答案.
解答 解:(1)∵BF为⊙O的切线,
∴∠ABF=90°,
∵∠BCD=∠BAD,
∴在Rt△ABF中,cos∠BCD=cos∠BAF=$\frac{AB}{AF}$=$\frac{3}{4}$,
∴AB=$\frac{3}{4}$AF=$\frac{3}{4}$×5=$\frac{15}{4}$,
∴AO=$\frac{1}{2}$AB=$\frac{15}{8}$;
(2)连结BD,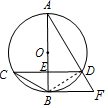
在Rt△ABD中,AD=ABcos∠BAD=$\frac{15}{4}$×$\frac{3}{4}$=$\frac{45}{16}$,
在Rt△ABF中,BF=$\sqrt{A{F}^{2}-A{B}^{2}}$=$\frac{5\sqrt{7}}{4}$,sin∠BAF=$\frac{BF}{AF}$=$\frac{\frac{5\sqrt{7}}{4}}{5}$=$\frac{\sqrt{7}}{4}$,
∴ED=ADsin∠EAD=$\frac{45}{16}$×$\frac{\sqrt{7}}{4}$=$\frac{45}{64}$$\sqrt{7}$,CD=2ED=$\frac{45}{32}$$\sqrt{7}$.
点评 本题主要考查切线的性质、勾股定理、垂径定理及解直角三角形,熟练掌握切线的性质和垂径定理及解直角三角形是解题的关键.

| A. | a>-$\frac{1}{5}$ | B. | -$\frac{1}{5}$<a<0 | C. | a<$\frac{1}{5}$ | D. | 0<a<$\frac{1}{5}$ |
| A. | a=5,b=1 | B. | a=-5,b=1 | C. | a=5,b=-1 | D. | a=-5,b=-1 |
| 众数 | 中位数 | 平均数 | 方差 |
| 8.5 | 8.3 | 8.1 | 0.15 |
| A. | 平均数 | B. | 中位数 | C. | 众数 | D. | 方差 |
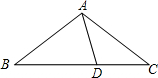 如图,在△ABC中,AB=AC,D为BC上一点,且DA=DC,BD=BA,则∠B的大小为( )
如图,在△ABC中,AB=AC,D为BC上一点,且DA=DC,BD=BA,则∠B的大小为( )| A. | 40° | B. | 36° | C. | 30° | D. | 25° |
 在平面直角坐标系xOy中,点P与点Q不重合,以点P为圆心作经过Q的圆,则称该圆为点P、Q的“相关圆”
在平面直角坐标系xOy中,点P与点Q不重合,以点P为圆心作经过Q的圆,则称该圆为点P、Q的“相关圆”