题目内容
11.m与n为何整数时,方程2x2-2mx+n=0的两根x1,x2满足1≤x1<2,2≤x2<3?分析 根据抛物线的性质列出关于m、n的不等式组,通过解不等式组求得m、n的值.
解答  解:由题意知,1<-$\frac{-2m}{4}$<3,则2<m<6.
解:由题意知,1<-$\frac{-2m}{4}$<3,则2<m<6.
∵m∈Z,
∴m=3,4,5,且$\left\{\begin{array}{l}{4{m}^{2}-8n≥0}\\{2-2m+n≥0}\\{8-4m+n≤0}\\{18-6m+n≥0}\end{array}\right.$,
把m=3,4,5分别代入,满足条件是:$\left\{\begin{array}{l}{m=4}\\{n=7}\end{array}\right.$或$\left\{\begin{array}{l}{m=5}\\{n=12}\end{array}\right.$.
点评 本题考查了抛物线与x轴的交点.熟练掌握一元二次方程根的分布是解题的关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 在筝形ABCD中,AD=CD,AB=BC,若∠ADC=∠ABC,∠DAC=45°,求证:筝形ABCD是正方形.
在筝形ABCD中,AD=CD,AB=BC,若∠ADC=∠ABC,∠DAC=45°,求证:筝形ABCD是正方形.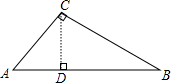 如图,用长3m、4m、5m的三根木棒正好搭成一个Rt△ABC,AC=3,∠C=90°,用一束垂直于AB的平行光线照上去,AC、BC在AB的影长分别为AD、DB,则AD=$\frac{9}{5}$,BD=$\frac{16}{5}$.
如图,用长3m、4m、5m的三根木棒正好搭成一个Rt△ABC,AC=3,∠C=90°,用一束垂直于AB的平行光线照上去,AC、BC在AB的影长分别为AD、DB,则AD=$\frac{9}{5}$,BD=$\frac{16}{5}$. 某空中加油机接到命令,立即给一架正在飞行的运输机进行空中加油,在加油过程中,设运输机机油箱的余油量为Q1吨,加油机的加油邮箱余油量为Q2吨,加油时间为t分钟,Q1,Q2与t之间的关系如图所示,结合图象回答问题:加油机的加油油箱中装载了多少吨油?将这些油全部加给运输机需要多少分钟?
某空中加油机接到命令,立即给一架正在飞行的运输机进行空中加油,在加油过程中,设运输机机油箱的余油量为Q1吨,加油机的加油邮箱余油量为Q2吨,加油时间为t分钟,Q1,Q2与t之间的关系如图所示,结合图象回答问题:加油机的加油油箱中装载了多少吨油?将这些油全部加给运输机需要多少分钟?