题目内容
19. 在筝形ABCD中,AD=CD,AB=BC,若∠ADC=∠ABC,∠DAC=45°,求证:筝形ABCD是正方形.
在筝形ABCD中,AD=CD,AB=BC,若∠ADC=∠ABC,∠DAC=45°,求证:筝形ABCD是正方形.
分析 利用等腰三角形的性质得出∠DAC=∠DCA=45°,进而得出∠BAD=∠ADC=∠DCB=∠ABC=90°,求出筝形ABCD是矩形,再利用邻边相等的矩形是正方形,进而得出答案.
解答 证明:∵AD=DC,∠DAC=45°,
∴∠DAC=∠DCA=45°,
∴∠ADC=∠ABC=90°,
∵AB=BC,
∴∠BAC=∠BCA=45°,
∴∠BAD=∠ADC=∠DCB=∠ABC=90°,
∴筝形ABCD是矩形,
又∵AD=DC,
∴筝形ABCD是正方形.
点评 此题主要考查了正方形的判定以及等腰三角形的性质等知识,熟练应用等腰三角形的性质得出∠DAC=∠DCA=∠BAC=∠BCA=45°是解题关键.

练习册系列答案
相关题目
10.分式方程$\frac{x}{x-3}$-$\frac{x+1}{x-1}$=0的解为( )
| A. | x=1 | B. | x=-1 | C. | x=3 | D. | x=-3 |
14.下列运算正确的是( )
| A. | x2+x2=2x4 | B. | x4•x2=x6 | C. | 3x2÷x=2x | D. | (x2)3=x5 |
 如图,某校A距离公路3千米,又与该公路旁上的某车站D的距离为5千米,现在公路边建一个商店C,使之与该校A及车站D的距离相等,则商店与车站的距离为$\frac{25}{8}$千米.
如图,某校A距离公路3千米,又与该公路旁上的某车站D的距离为5千米,现在公路边建一个商店C,使之与该校A及车站D的距离相等,则商店与车站的距离为$\frac{25}{8}$千米.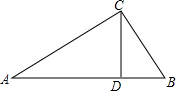 如图,在Rt△ABC中,∠C=90°,CD⊥AB,垂足为D,AD=8,DB=2,则CD的长为4.
如图,在Rt△ABC中,∠C=90°,CD⊥AB,垂足为D,AD=8,DB=2,则CD的长为4. 如图,在△ABC中,EF⊥AB,CD⊥AB,G在AC上,∠CDG=∠BEF,试说明∠AGD=∠ACB.
如图,在△ABC中,EF⊥AB,CD⊥AB,G在AC上,∠CDG=∠BEF,试说明∠AGD=∠ACB.