题目内容
3.已知a=3-$\sqrt{2}$,b=3+$\sqrt{2}$,试求$\frac{b}{a}$-$\frac{a}{b}$的值.分析 将a,b的值代入化简即可.
解答 解:∵a=3-$\sqrt{2}$,b=3+$\sqrt{2}$,
∴$\frac{b}{a}$-$\frac{a}{b}$=$\frac{3+\sqrt{2}}{3-\sqrt{2}}$$-\frac{3-\sqrt{2}}{3+\sqrt{2}}$=$\frac{{(3+\sqrt{2})}^{2}}{(3-\sqrt{2})(3+\sqrt{2})}$-$\frac{{(3-\sqrt{2})}^{2}}{(3+\sqrt{2})(3-\sqrt{2})}$=$\frac{12\sqrt{2}}{7}$.
点评 本题主要考查了二次根式的化简,将二次根式分母有理化是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.下列运算正确的是( )
| A. | x2+x2=2x4 | B. | x4•x2=x6 | C. | 3x2÷x=2x | D. | (x2)3=x5 |
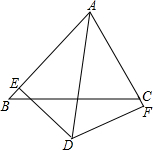 已知在△ABC中,∠BAC的平分线与BC的垂直平分线相交于点D,DE⊥AB于点E,DF⊥AC交AC的延长线于点F,求证:BE=CF.
已知在△ABC中,∠BAC的平分线与BC的垂直平分线相交于点D,DE⊥AB于点E,DF⊥AC交AC的延长线于点F,求证:BE=CF. 如图,四边形OABC的边OA,OC分别在y轴、x轴的正半轴,且OA=OC=3,∠OCB=90°,AB=$\sqrt{10}$.
如图,四边形OABC的边OA,OC分别在y轴、x轴的正半轴,且OA=OC=3,∠OCB=90°,AB=$\sqrt{10}$.