题目内容
17.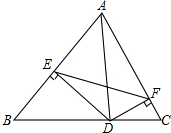 △ABC中,AD⊥BC于点D,DE⊥AC于E,DF⊥AB于点F,求证:∠AFE=∠B.
△ABC中,AD⊥BC于点D,DE⊥AC于E,DF⊥AB于点F,求证:∠AFE=∠B.
分析 先根据射影定理AD2=AE•AB,AD2=AF•AC.所以AE•AB=AF•AC,进而可得出结论.
解答 证明:∵在△ABC中,AD⊥BC于D,DE⊥AC于E,DF⊥AB于F,
∴在Rt△ABD中,AD2=AE•AB.
同理可得,AD2=AF•AC,
∴AE•AB=AF•AC,即$\frac{AE}{AC}=\frac{AF}{AB}$,
∵∠BAC是公共角,
∴△AEF∽△ACB,
∴∠AEF=∠B.
点评 本题考查的是相似三角形的判定,熟知两组对应边的比相等且夹角对应相等的两个三角形相似是解答此题的关键.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
 如图是一个全由棱长为1的正方体堆积而成的几何体的俯视图,俯视图上的数字表示此位置的小立方块的个数,求这个几何体的表面积.
如图是一个全由棱长为1的正方体堆积而成的几何体的俯视图,俯视图上的数字表示此位置的小立方块的个数,求这个几何体的表面积.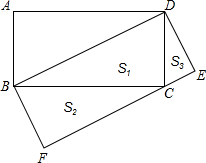 如图,矩形ABCD中,以对角线BD为一边构造一个矩形BDEF,使得另一边EF过原矩形的顶点C.
如图,矩形ABCD中,以对角线BD为一边构造一个矩形BDEF,使得另一边EF过原矩形的顶点C.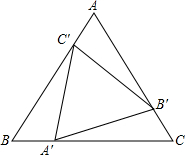 已知:如图所示,点A′,B′,C′分别在等边三角形ABC的三边上,且AC′=BA′=CB′,求证:△A′B′C′是等边三角形.
已知:如图所示,点A′,B′,C′分别在等边三角形ABC的三边上,且AC′=BA′=CB′,求证:△A′B′C′是等边三角形.