题目内容
2.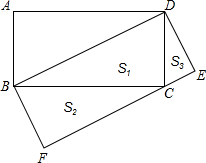 如图,矩形ABCD中,以对角线BD为一边构造一个矩形BDEF,使得另一边EF过原矩形的顶点C.
如图,矩形ABCD中,以对角线BD为一边构造一个矩形BDEF,使得另一边EF过原矩形的顶点C.(1)设Rt△CBD的面积为S1,Rt△BFC的面积为S2,Rt△DCE的面积为S3,则S1=S2+S3(用“>”、“=”、“<”填空);
(2)写出图中的三对相似(不全等)三角形;
(3)求证:BC2=CF•DB(尽可能用数字表示角)
分析 (1)根据S1=$\frac{1}{2}$S矩形BDEF,S2+S3=$\frac{1}{2}$S矩形BDEF,即可得出答案.
(2)根据矩形的性质,结合图形可得:△BCD∽△CFB∽△DEC;
(3)由四边形BDEF是矩形,得到∠CBF+∠DBC=90°,∠CBD+∠BDC=90°,于是得到∠BCF=∠CBD,证得△BCD∽△BCF,得到比例式,即可得到结论.
解答 解:(1)∵S1=$\frac{1}{2}$BD×ED,S矩形BDEF=BD×ED,
∴S1=$\frac{1}{2}$S矩形BDEF,
∴S2+S3=$\frac{1}{2}$S矩形BDEF,
∴S1=S2+S3;
故答案为:=.
(2)答:△BCD∽△CFB∽△DEC;
(3)∵四边形BDEF是矩形,
∴∠CBF+∠DBC=90°,∠CBD+∠BDC=90°,
∴∠BCF=∠CBD,
又∵∠BCD=∠F=90°,
∴△BCD∽△BCF,
∴$\frac{BC}{BD}=\frac{CF}{BC}$,
∴BC2=CF•DB.
点评 本题考查了相似三角形的判定和性质,矩形的性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
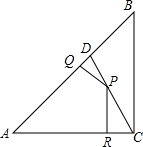 已知如图:在△ABC中,AC=BC,∠ACB=90°,AD=AC,点P是CD上任意一点,PQ⊥AB于Q,PR⊥AC于R,求证:PQ+PR=$\frac{1}{2}$AB.
已知如图:在△ABC中,AC=BC,∠ACB=90°,AD=AC,点P是CD上任意一点,PQ⊥AB于Q,PR⊥AC于R,求证:PQ+PR=$\frac{1}{2}$AB.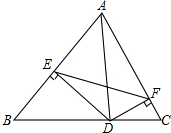 △ABC中,AD⊥BC于点D,DE⊥AC于E,DF⊥AB于点F,求证:∠AFE=∠B.
△ABC中,AD⊥BC于点D,DE⊥AC于E,DF⊥AB于点F,求证:∠AFE=∠B.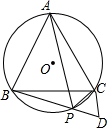 如图,等边△ABC内接于⊙O,点P是劣弧$\widehat{BC}$上的一点(端点除外),延长BP至D,使BD=AP,连CD,请你判断△PDC是什么三角形?并说明理由.
如图,等边△ABC内接于⊙O,点P是劣弧$\widehat{BC}$上的一点(端点除外),延长BP至D,使BD=AP,连CD,请你判断△PDC是什么三角形?并说明理由. 如图,已知AD是△ABC的角平分线,且AC=AB+BD,∠C=30°,求∠BAC的度数.
如图,已知AD是△ABC的角平分线,且AC=AB+BD,∠C=30°,求∠BAC的度数.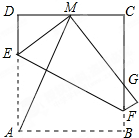 将边长为10正方形ABCD折叠,使顶点A与CD边上的点M重合,折痕交AD于E,交BC于F,边AB折叠后与BC边交于点G.
将边长为10正方形ABCD折叠,使顶点A与CD边上的点M重合,折痕交AD于E,交BC于F,边AB折叠后与BC边交于点G.