题目内容
18.(1)问题发现:如图①,在等边三角形ABC中,点M为BC边上异于B、C的一点,以AM为边作等边三角形AMN,连接CN,NC与AB的位置关系为NC∥AB;
(2)深入探究:
如图②,在等腰三角形ABC中,BA=BC,点M为BC边上异于B、C的一点,以AM为边作等腰三角形AMN,使∠ABC=∠AMN,AM=MN,连接CN,试探究∠ABC与∠ACN的数量关系,并说明理由;
(3)拓展延伸:
如图③,在正方形ADBC中,AD=AC,点M为BC边上异于B、C的一点,以AM为边作正方形AMEF,点N为正方形AMEF的中点,连接CN,若BC=10,CN=$\sqrt{2}$,试求EF的长.

分析 (1)根据△ABC,△AMN为等边三角形,得到AB=AC,AM=AN且∠BAC=∠MAN=60°从而得到∠BAC-∠CAM=∠MAN-∠CAM,即∠BAM=∠CAN,证明△BAM≌△CAN,即可得到BM=CN.
(2)根据△ABC,△AMN为等腰三角形,得到AB:BC=1:1且∠ABC=∠AMN,根据相似三角形的性质得到$\frac{AB}{AM}=\frac{AC}{AN}$,利用等腰三角形的性质得到∠BAC=∠MAN,根据相似三角形的性质即可得到结论;
(3)如图3,连接AB,AN,根据正方形的性质得到∠ABC=∠BAC=45°,∠MAN=45°,根据相似三角形的性质得出$\frac{BM}{CN}=\frac{AB}{AC}$,得到BM=2,CM=8,再根据勾股定理即可得到答案.
解答 解:(1)NC∥AB,理由如下:
∵△ABC与△MN是等边三角形,
∴AB=AC,AM=AN,∠BAC=∠MAN=60°,
∴∠BAM=∠CAN,
在△ABM与△ACN中,$\left\{\begin{array}{l}{AB=AC}&{\;}\\{∠BAM=∠CAN}&{\;}\\{AM=AN}&{\;}\end{array}\right.$,
∴△ABM≌△ACN(SAS),
∴∠B=∠ACN=60°,
∵∠ANC+∠ACN+∠CAN=∠ANC+60°+∠CAN=180°,
∴∠ANC+∠MAN+∠BAM=∠ANC+60°+∠CAN=∠BAN+∠ANC=180°,
∴CN∥AB;
故答案为:CN∥AB;
(2)∠ABC=∠ACN,理由如下:
∵$\frac{AB}{BC}=\frac{AM}{MN}$=1且∠ABC=∠AMN,
∴△ABC~△AMN
∴$\frac{AB}{AM}=\frac{AC}{AN}$,
∵AB=BC,
∴∠BAC=$\frac{1}{2}$(180°-∠ABC),
∵AM=MN
∴∠MAN=$\frac{1}{2}$(180°-∠AMN),
∵∠ABC=∠AMN,
∴∠BAC=∠MAN,
∴∠BAM=∠CAN,
∴△ABM~△ACN,
∴∠ABC=∠ACN;
(3)如图3,连接AB,AN,
∵四边形ADBC,AMEF为正方形,
∴∠ABC=∠BAC=45°,∠MAN=45°,
∴∠BAC-∠MAC=∠MAN-∠MAC
即∠BAM=∠CAN,
∵$\frac{AB}{AC}=\frac{AM}{AN}$=$\sqrt{2}$,
∴$\frac{AB}{AM}=\frac{AC}{AN}$,
∴△ABM~△ACN
∴$\frac{BM}{CN}=\frac{AB}{AC}$,
∴$\frac{CN}{BM}=\frac{AC}{AB}$=cos45°=$\frac{\sqrt{2}}{2}$,
∴$\frac{\sqrt{2}}{BM}$=$\frac{\sqrt{2}}{2}$,
∴BM=2,∴CM=BC-BM=8,
在Rt△AMC,
AM=$\sqrt{A{C}^{2}+M{C}^{2}}$=$\sqrt{1{0}^{2}+{8}^{2}}$=2$\sqrt{41}$,
∴EF=AM=2$\sqrt{41}$.
点评 本题是四边形综合题目,考查了正方形的性质、等边三角形的性质、等腰三角形的性质、全等三角形的性质定理和判定定理、相似三角形的性质定理和判定定理等知识;本题综合性强,有一定难度,证明三角形全等和三角形相似是解决问题的关键.

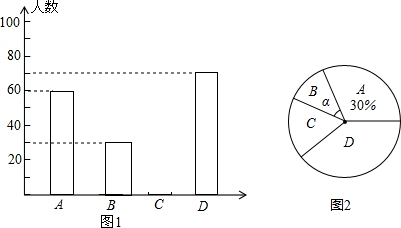
 请根据下列图表信息解答问题:
请根据下列图表信息解答问题:| 年份 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 |
| 年增长率 | 31% | 27% | 32% | 35% | 52% |
(2)求统计表中增长率的平均数及中位数;
(3)预测2017年的观影人次,并说明理由.
 如图,C、D是以线段AB为直径的⊙O上两点,若CA=CD,且∠CAB=25°,则∠ACD的度数为( )
如图,C、D是以线段AB为直径的⊙O上两点,若CA=CD,且∠CAB=25°,则∠ACD的度数为( )| A. | 25° | B. | 30° | C. | 40° | D. | 50° |
| A. | x>1 | B. | x>1且x≠2 | C. | x≥1且x≠2 | D. | x≠2 |
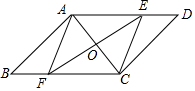 如图,在?ABCD中,对角线AC的垂直平分线EF与AC交于点O,与AD交于点E,与BC交于点F,连接EC,AF,
如图,在?ABCD中,对角线AC的垂直平分线EF与AC交于点O,与AD交于点E,与BC交于点F,连接EC,AF,