题目内容

13．先化简，再求值：
（$\frac{a-2}{{a}^{2}+2a}$-$\frac{a-1}{{a}^{2}+4a+4}$）÷（$\frac{a-4}{a+2}$），其中a满足：$\frac{1}{2}$a2+a-4=0．

分析 先根据分式混合运算的法则把原式进行化简，再由$\frac{1}{2}$a2+a-4=0得到a2+2a=8代入即可．

解答 解：（$\frac{a-2}{{a}^{2}+2a}$-$\frac{a-1}{{a}^{2}+4a+4}$）÷（$\frac{a-4}{a+2}$）=[$\frac{a-2}{a（a+2）}$-$\frac{a-1}{（a+2）^{2}}$]•$\frac{a+2}{a-4}$=a2+2a，
∵$\frac{1}{2}$a2+a-4=0，
∴a2+2a-8=0
∴a2+2a=8．

点评 本题考查的是分式的化简求值，熟知分式混合运算的法则是解答此题的关键．

练习册系列答案
相关题目
3．如图，AC是矩形ABCD的对角线，过AC的中点O作EF⊥AC，交BC于点E，交AD于点F，连接AE，CF．
（1）求证：四边形AECF是菱形；
（2）若AB=$\sqrt{6}$，cos∠DCF=$\frac{\sqrt{3}}{2}$，求四边形AECF的面积．（结果保留根号）
4．据中古江西网报道，4月22日全省将有近15万人参加2017年省公务员录用考试笔试，数字15万用科学记数法表示为：1.5×105．
1．为迎接2017年普通高中招生体育加试，某中学在3月份对全校九年级400名学生进行了一次体育摸底测试，随机抽取了部分学生的测试成绩作为样本进行分析，并绘制成了如下两幅不完整的统计图．
请根据图中所给信息，解答下列问题：
（1）请将表示成绩类别为“中”的条形统计图补充完整；
（2）在条形统计图中成绩类别的中位数落在良这一段（填“优”，“良”，“中”，“差”），在扇形统计图中，表示成绩类别为“优”的扇形所对应的圆心角是72度；
（3）估计该校九年级学生的体育成绩可以达到良好和优秀共有多少名？
8．如图1，ABCD为正方形，将正方形的边CB绕点C顺时针旋转到CE，记∠BCE=α，连接BE，DE，过点C作CF⊥DE于F，交直线BE于H．
（1）当α=60°时，如图1，则∠BHC=45°；
（2）当45°＜α＜90°，如图2，线段BH、EH、CH之间存在一种特定的数量关系，请你通过探究，写出这个关系式：BH+EH=$\sqrt{2}$CH（不需证明）；
（3）当90°＜α＜180°，其它条件不变（如图3），（2）中的关系式是否还成立？若成立，说明理由；若不成立，写出你认为成立的结论，并简要证明．
18．（1）问题发现：
如图①，在等边三角形ABC中，点M为BC边上异于B、C的一点，以AM为边作等边三角形AMN，连接CN，NC与AB的位置关系为NC∥AB；
（2）深入探究：
如图②，在等腰三角形ABC中，BA=BC，点M为BC边上异于B、C的一点，以AM为边作等腰三角形AMN，使∠ABC=∠AMN，AM=MN，连接CN，试探究∠ABC与∠ACN的数量关系，并说明理由；
（3）拓展延伸：
如图③，在正方形ADBC中，AD=AC，点M为BC边上异于B、C的一点，以AM为边作正方形AMEF，点N为正方形AMEF的中点，连接CN，若BC=10，CN=$\sqrt{2}$，试求EF的长．
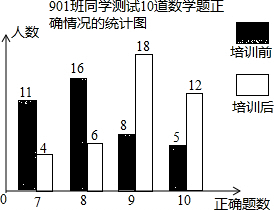5．小潘老师为了检测901班同学培训效果做了一项教学实验：通过测试10道数学题了解培训前和培训后学生的解题情况．并绘成如下的条形统计图．根据统计图，回答下列问题：
（1）求培训后正确题数的中位数、众数；
（2）若正确题数不少于9道为优秀，求培训前、培训后的优秀率；
（3）请选择适当的统计量，从两个不同的角度评价培训的效果．
9．如图，直线a，b被直线c所截，若∠1+∠2=180°，判断直线a与b是否平行，并说明理由．
10．如图，四边形ABCD是一个菱形绿地，其周长为40$\sqrt{2}$ m，∠ABC=120°，在其内部有一个四边形花坛EFGH，其四个顶点恰好在菱形ABCD各边的中点，现在准备在花坛中种植茉莉花，其单价为10元/m2，请问需投资金多少元？（结果保留整数）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网