题目内容
在Rt△ABC中，∠C=90°，tanA=
，则sinB的值为 ．
| 5 |
| 12 |
考点：互余两角三角函数的关系
专题：
分析：作出草图，根据∠A的正切值设出两直角边分别为5k，12k，然后利用勾股定理求出斜边，则∠B的正弦值即可求出．
解答：
解：如图，∵在Rt△ABC中，∠C=90°，tanA=
，
∴设AC=12k，BC=5k，
则AB=
=13k，
∴sinB=
=
=
．
故答案为：
．
解：如图，∵在Rt△ABC中，∠C=90°，tanA=| 5 |
| 12 |
∴设AC=12k，BC=5k，
则AB=
| (12k)2+(5k)2 |
∴sinB=
| AC |
| AB |
| 12k |
| 13k |
| 12 |
| 13 |
故答案为：
| 12 |
| 13 |
点评：本题考查了互余两角的三角函数的关系，作出草图，利用数形结合思想更形象直观，此类题目通常都用到勾股定理．
练习册系列答案
智能训练练测考系列答案
相关题目
如图所示，PA、PB为⊙O的切线，M、N是PA、AB的中点，连接MN交⊙O点C，连接PC交⊙O于D，连接ND交PB于Q，求证：MNQP为菱形．
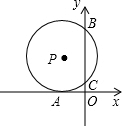如图，⊙P的圆心在第二象限内，且与x轴相切于点A，与y轴相交于B（0，8）、C（0，2），则圆心P的坐标是（ ）| A、（-3，4） |
| B、（-4，6） |
| C、（-3，5） |
| D、（-4，5） |
如图，在△ABC中，D、E分别是边AC和AB上的点，且DE≠BC，请你添加一个条件，使得△ABC与△AED相似，你添加的条件是