题目内容
 如图,在△ABC中,D、E分别是边AC和AB上的点,且DE≠BC,请你添加一个条件,使得△ABC与△AED相似,你添加的条件是
如图,在△ABC中,D、E分别是边AC和AB上的点,且DE≠BC,请你添加一个条件,使得△ABC与△AED相似,你添加的条件是考点:相似三角形的判定
专题:开放型
分析:由条件可知△ABC和△ADE有公共角,根据三角形相似的判定方法可再添加一组角对应相等,或添加∠EAD和∠BAC的两边对应成比例,或添加ED∥BC.
解答:解:在△ABC和△AED中,
因为∠EAD=∠BAC,
故只需要增加一组角对应相等即可,
可添加∠AED=∠ACB,
此时△ABC∽△ADE,
也可添加∠AED=∠ABC,或
=
或
=
或DE∥BC都可以,
故答案为:∠AED=∠ACB(∠AED=∠ABC或
=
或
=
或DE∥BC).
因为∠EAD=∠BAC,
故只需要增加一组角对应相等即可,
可添加∠AED=∠ACB,
此时△ABC∽△ADE,
也可添加∠AED=∠ABC,或
| AE |
| AC |
| AD |
| AB |
| AE |
| AB |
| AD |
| AC |
故答案为:∠AED=∠ACB(∠AED=∠ABC或
| AE |
| AC |
| AD |
| AB |
| AE |
| AB |
| AD |
| AC |
点评:本题主要考查三角形相似的判定,掌握相似三角形的判定方法是解题的关键.

练习册系列答案
相关题目
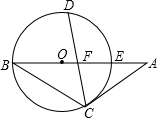 如图,以△ABC的边AB上一点O为圆心的圆经过B、C两点,且与边AB相交于点E,D是弧BE的中点,CD交AB于F,AC=AF.
如图,以△ABC的边AB上一点O为圆心的圆经过B、C两点,且与边AB相交于点E,D是弧BE的中点,CD交AB于F,AC=AF.(1)求证:AC是⊙O的切线;
(2)若EF=5,DF=
| 37 |
下列各式从左到右的变形中,是因式分解的是( )
| A、3x+2x-1=5x-1 | ||
| B、(3a+2b)(3a-2b)=9a2-4b2 | ||
C、x2+x=x2(1+
| ||
| D、2x2-8y2=2(x+2y)(x-2y) |
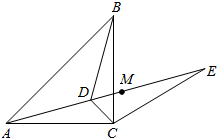 如图,已知点D为等腰直角△ABC内一点,∠BAD=∠ABD=30°,E为AD延长线上的一点,且CE=CA.
如图,已知点D为等腰直角△ABC内一点,∠BAD=∠ABD=30°,E为AD延长线上的一点,且CE=CA.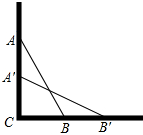 一架云梯AB长25米,如图那样斜靠在一面墙AC上,这时云梯底端B离墙底C的距离BC为7米.
一架云梯AB长25米,如图那样斜靠在一面墙AC上,这时云梯底端B离墙底C的距离BC为7米. 如图,已知在Rt△ABC中,∠C=90°,AC=12,BC=9,D是AB上一点,以BD为直径的⊙O切AC于E,求AD的长.
如图,已知在Rt△ABC中,∠C=90°,AC=12,BC=9,D是AB上一点,以BD为直径的⊙O切AC于E,求AD的长.