题目内容
已知函数y=ax2的图象过点(1,-
).
(1)简述函数的性质;
(2)在图象上有两点(x1,y1),(x2,y2),且x1>x2>0,比较y1,y2的大小.
| 1 |
| 2 |
(1)简述函数的性质;
(2)在图象上有两点(x1,y1),(x2,y2),且x1>x2>0,比较y1,y2的大小.
考点:二次函数的性质,二次函数图象上点的坐标特征
专题:
分析:(1)把点(1,-
)代入函数y=ax2的解析式求得a的值,即可判定函数的性质.
(2)二次函数y=ax2对称轴为y轴;当x1>x2>0,时,在对称轴的同侧,根据二次函数图象的性质,在对称轴的右侧y随x的增大而减小,故y1<y2.
| 1 |
| 2 |
(2)二次函数y=ax2对称轴为y轴;当x1>x2>0,时,在对称轴的同侧,根据二次函数图象的性质,在对称轴的右侧y随x的增大而减小,故y1<y2.
解答:解:(1)∵函数y=ax2的图象过点(1,-
).
∴a=-
,
∴开口向下,对称轴为y轴,在y轴的右侧y随x的增大而减小,在y轴的左侧y随x的增大而增大.
(2)∵该抛物线上两点(x1,y1)、(x2,y2)的且x1>x2>0,
∵x>0时,y随x的增大而减小,
∵x1>x2>0,
∴y1<y2.
| 1 |
| 2 |
∴a=-
| 1 |
| 2 |
∴开口向下,对称轴为y轴,在y轴的右侧y随x的增大而减小,在y轴的左侧y随x的增大而增大.
(2)∵该抛物线上两点(x1,y1)、(x2,y2)的且x1>x2>0,
∵x>0时,y随x的增大而减小,
∵x1>x2>0,
∴y1<y2.
点评:本题考查了二次函数的性质,二次函数图象上点的坐标特征,本题的关键是掌握二次函数的图象性质.

练习册系列答案
相关题目
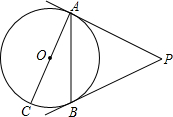 如图,PA、PB是⊙O的切线,A、B为切点,AC是⊙O的直径且AC=6,∠P=50°,求
如图,PA、PB是⊙O的切线,A、B为切点,AC是⊙O的直径且AC=6,∠P=50°,求
 如图,圆O的直径AB垂直于弦CD,垂足是E,∠A=22.5°,OC=4,CD的长为
如图,圆O的直径AB垂直于弦CD,垂足是E,∠A=22.5°,OC=4,CD的长为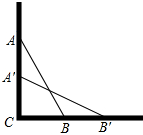 一架云梯AB长25米,如图那样斜靠在一面墙AC上,这时云梯底端B离墙底C的距离BC为7米.
一架云梯AB长25米,如图那样斜靠在一面墙AC上,这时云梯底端B离墙底C的距离BC为7米.