题目内容
已知函数y=-
x2与y=-ax2+c(a≠0)的图象完全相同,且抛物线y=-
x2的图象沿对称轴平移两个单位后就能与y=-ax2+c的图象完全重合,求平移后的二次函数的表达式.
| 2 |
| 3 |
| 2 |
| 3 |
考点:二次函数图象与几何变换
专题:
分析:由函数y=-
x2与y=-ax2+c(a≠0)的图象完全相同,可知a=
,由抛物线y=-
x2的对称轴为y轴,根据上加下减的平移规律即可求解.
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
解答:解:∵函数y=-
x2与y=-ax2+c(a≠0)的图象完全相同,
∴a=
,
又∵抛物线y=-
x2的对称轴为y轴,
∴抛物线y=-
x2的图象沿对称轴平移两个单位后就能与y=-ax2+c的图象完全重合,
∴平移后的二次函数的表达式为y=-
x2±2.
| 2 |
| 3 |
∴a=
| 2 |
| 3 |
又∵抛物线y=-
| 2 |
| 3 |
∴抛物线y=-
| 2 |
| 3 |
∴平移后的二次函数的表达式为y=-
| 2 |
| 3 |
点评:本题考查的是二次函数的图象与几何变换,熟知图形平移不变性的性质是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列各式从左向右变形,属于因式分解的是( )
| A、a(a-b+1)=a2-ab+a | ||
B、a2-a-2=a(a-1-
| ||
| C、-4a2+9b2=(-2a+3b)(2a+3b) | ||
| D、x2-4x-5=(x-2)2-9 |
 如图、用圆规比较下列线段的大小:AO
如图、用圆规比较下列线段的大小:AO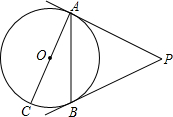 如图,PA、PB是⊙O的切线,A、B为切点,AC是⊙O的直径且AC=6,∠P=50°,求
如图,PA、PB是⊙O的切线,A、B为切点,AC是⊙O的直径且AC=6,∠P=50°,求
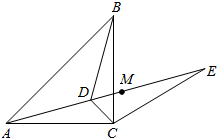 如图,已知点D为等腰直角△ABC内一点,∠BAD=∠ABD=30°,E为AD延长线上的一点,且CE=CA.
如图,已知点D为等腰直角△ABC内一点,∠BAD=∠ABD=30°,E为AD延长线上的一点,且CE=CA.