题目内容
 如图所示,PA、PB为⊙O的切线,M、N是PA、AB的中点,连接MN交⊙O点C,连接PC交⊙O于D,连接ND交PB于Q,求证:MNQP为菱形.
如图所示,PA、PB为⊙O的切线,M、N是PA、AB的中点,连接MN交⊙O点C,连接PC交⊙O于D,连接ND交PB于Q,求证:MNQP为菱形.考点:切线的性质,菱形的判定
专题:证明题
分析:首先连接OA,OB,OC,OD,OP.由M、N是PA、AB的中点,根据三角形中位线的性质,可得MN∥BP,又由PA、PB为⊙O的切线,可得AB⊥OP,即可证得MN=PM,然后由射影定理与切割线定理证得O,C,D,N四点共圆,继而证得MP∥NQ,则可得四边形MNQP是平行四边形,证得四边形MNQP是菱形.
解答: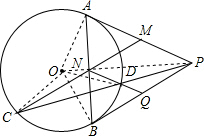 证明:连接OA,OB,OC,OD,OP.
证明:连接OA,OB,OC,OD,OP.
∵AN=NB,AM=MP.
∴MN∥BP.
∵PA、PB为⊙O的切线,
∴AB⊥OP.
∴NM=MP,∠MNP=∠MPN,
在Rt△AOP中,由射影定理,得AP2=PN•PO,
由切割线定理,得AP2 =PD•PC,
∴PN•PO=PD•PC,
∴O,C,D,N四点共圆,
∴∠PND=∠OCD,∠ONC=∠ODC,
∵OC=OD,
∴∠OCD=∠ODC,
∵∠MNP=∠ONC,
∴∠MNP=∠PND=∠MPN,
∴MP∥NQ,
∴四边形MNQP是平行四边形,
∴四边形MNQP是菱形.
 证明:连接OA,OB,OC,OD,OP.
证明:连接OA,OB,OC,OD,OP.∵AN=NB,AM=MP.
∴MN∥BP.
∵PA、PB为⊙O的切线,
∴AB⊥OP.
∴NM=MP,∠MNP=∠MPN,
在Rt△AOP中,由射影定理,得AP2=PN•PO,
由切割线定理,得AP2 =PD•PC,
∴PN•PO=PD•PC,
∴O,C,D,N四点共圆,
∴∠PND=∠OCD,∠ONC=∠ODC,
∵OC=OD,
∴∠OCD=∠ODC,
∵∠MNP=∠ONC,
∴∠MNP=∠PND=∠MPN,
∴MP∥NQ,
∴四边形MNQP是平行四边形,
∴四边形MNQP是菱形.
点评:此题考查了切线的性质、三角形中位线的性质、射影定理、切割线定理以及菱形的判定.此题难度较大,综合性较强,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
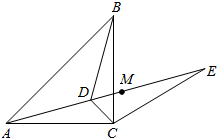 如图,已知点D为等腰直角△ABC内一点,∠BAD=∠ABD=30°,E为AD延长线上的一点,且CE=CA.
如图,已知点D为等腰直角△ABC内一点,∠BAD=∠ABD=30°,E为AD延长线上的一点,且CE=CA. 如图,圆O的直径AB垂直于弦CD,垂足是E,∠A=22.5°,OC=4,CD的长为
如图,圆O的直径AB垂直于弦CD,垂足是E,∠A=22.5°,OC=4,CD的长为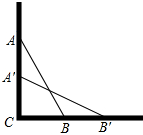 一架云梯AB长25米,如图那样斜靠在一面墙AC上,这时云梯底端B离墙底C的距离BC为7米.
一架云梯AB长25米,如图那样斜靠在一面墙AC上,这时云梯底端B离墙底C的距离BC为7米.