题目内容
14.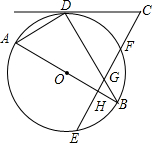 如图,AB是⊙O的直径,BD,EF是⊙O的弦,EF⊥AB于点H,交BD于点G,过点D的直线与EF的延长线交于点C,若△CDG是等边三角形.
如图,AB是⊙O的直径,BD,EF是⊙O的弦,EF⊥AB于点H,交BD于点G,过点D的直线与EF的延长线交于点C,若△CDG是等边三角形.(1)求证:CD是⊙O的切线;
(2)若AB=10,HB=2,求△CDG的周长.
分析 (1)连接OD,先证∠CDG=60°,再证出∠ODB=30°,得出∠ODC=90°,即可得出结论;
(2)根据锐角三角函数求出BD、BG,得出DG,即可求出周长.
解答 (1)证明:连接OD,如图所示: ∵△CDG是等边三角形,
∵△CDG是等边三角形,
∴∠CDG=∠CGD=60°,
∴∠BGH=∠CGD=60°,
∵EF⊥AB,
∴∠BHG=90°,
∴∠B=30°,
∵OD=OB,
∴∠ODB=∠B=30°,
∴∠ODB+∠CDG=90°,
即∠ODC=90°,
∴CD是⊙O的切线;
(2)解:∵AB是⊙O的直径,
∴∠ADB=90°,
∵AB=10,∠B=30°,
∴BD=AB•sin30°=5$\sqrt{3}$,
∵BG=$\frac{BH}{cos30°}$=$\frac{4\sqrt{3}}{3}$,
∴DG=5$\sqrt{3}$-$\frac{4\sqrt{3}}{3}$=$\frac{11\sqrt{3}}{3}$,
∴CDG的周长=3DG=11$\sqrt{3}$.
点评 本题考查了切线的判定、等边三角形的性质、锐角三角函数的运用;熟练掌握切线的判定方法,并能进行推理计算是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
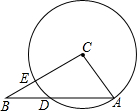 在△ABC中,∠B=30°,AC=10cm,BC=16cm,以点C为圆心,AC为半径的圆交AB于点D、交BC于点E.
在△ABC中,∠B=30°,AC=10cm,BC=16cm,以点C为圆心,AC为半径的圆交AB于点D、交BC于点E.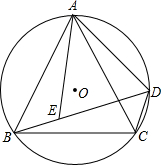 如图,△ABC内接于⊙O,AB=AC,D是弧AC上一点,连接BD,E是BD上一点,且BE=CD.
如图,△ABC内接于⊙O,AB=AC,D是弧AC上一点,连接BD,E是BD上一点,且BE=CD.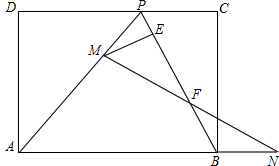 如图,已知矩形ABCD边CD上有一点P,且AP=AB,M是线段AP上的一点(不与点P、A重合),N是线段AB延长线上的一点,且BN=PM,连结MN交PB于点F,过点M作ME⊥BP于点E,若AD=8,PC=4,则线段EF的长是2$\sqrt{5}$.
如图,已知矩形ABCD边CD上有一点P,且AP=AB,M是线段AP上的一点(不与点P、A重合),N是线段AB延长线上的一点,且BN=PM,连结MN交PB于点F,过点M作ME⊥BP于点E,若AD=8,PC=4,则线段EF的长是2$\sqrt{5}$.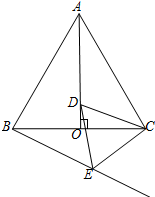 如图,等边△ABC的边长为6,AO⊥BC于D,D为AO上一点,以CD为一边且在CD下方作等边△CDE,连结BE.
如图,等边△ABC的边长为6,AO⊥BC于D,D为AO上一点,以CD为一边且在CD下方作等边△CDE,连结BE.