题目内容
6.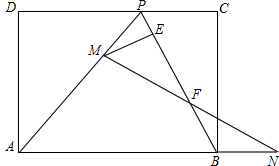 如图,已知矩形ABCD边CD上有一点P,且AP=AB,M是线段AP上的一点(不与点P、A重合),N是线段AB延长线上的一点,且BN=PM,连结MN交PB于点F,过点M作ME⊥BP于点E,若AD=8,PC=4,则线段EF的长是2$\sqrt{5}$.
如图,已知矩形ABCD边CD上有一点P,且AP=AB,M是线段AP上的一点(不与点P、A重合),N是线段AB延长线上的一点,且BN=PM,连结MN交PB于点F,过点M作ME⊥BP于点E,若AD=8,PC=4,则线段EF的长是2$\sqrt{5}$.
分析 作MQ∥AN,交PB于点Q,求出MP=MQ,BN=QM,得出MP=MQ,根据ME⊥PQ,得出EQ$\frac{1}{2}$PQ,根据∠QMF=∠BNF,证出△MFQ≌△NFB,得出QF$\frac{1}{2}$QB,
再求出EF$\frac{1}{2}$PB,由(1)中的结论求出PB=$\sqrt{{8}^{2}{+4}^{2}}$=4$\sqrt{5}$,即可得出线段EF的长度.
解答  解:如图作MQ∥AN,交PB于点Q,
解:如图作MQ∥AN,交PB于点Q,
∵AP=AB,MQ∥AN,
∴∠APB=∠ABP=∠MQP.
∴MP=MQ,
∵BN=PM,
∴BN=QM.
∵MP=MQ,ME⊥PQ,
∴EQ=$\frac{1}{2}$PQ.
∵MQ∥AN,
∴∠QMF=∠BNF,
在△MFQ和△NFB中,
$\left\{\begin{array}{l}{∠QFM=∠NFB}\\{∠QMF=∠BNF}\\{MQ=BN}\end{array}\right.$,
∴△MFQ≌△NFB(AAS).
∴QF=BF=$\frac{1}{2}$QB,
∴EF=EQ+QF=$\frac{1}{2}$PQ+$\frac{1}{2}$QB=$\frac{1}{2}$PB,
∵PC=4,BC=8,∠C=90°,
∴PB=$\sqrt{{8}^{2}{+4}^{2}}$=4$\sqrt{5}$,
∴EF=$\frac{1}{2}$PB=2$\sqrt{5}$.
点评 此题考查了全等三角形的判定与性质、勾股定理、等腰三角形的性质,关键是做出辅助线,找出全等的三角形.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
13.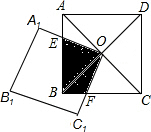 如图,正方形ABCD的对角线交于点O,点O又是正方形A1B1C1O的一个顶点,而且这两个正方形的边长相等.无论正方形A1B1C1O绕点O怎样转动,两个正方形重叠部分的面积,总等于一个正方形面积的( )
如图,正方形ABCD的对角线交于点O,点O又是正方形A1B1C1O的一个顶点,而且这两个正方形的边长相等.无论正方形A1B1C1O绕点O怎样转动,两个正方形重叠部分的面积,总等于一个正方形面积的( )
 如图,正方形ABCD的对角线交于点O,点O又是正方形A1B1C1O的一个顶点,而且这两个正方形的边长相等.无论正方形A1B1C1O绕点O怎样转动,两个正方形重叠部分的面积,总等于一个正方形面积的( )
如图,正方形ABCD的对角线交于点O,点O又是正方形A1B1C1O的一个顶点,而且这两个正方形的边长相等.无论正方形A1B1C1O绕点O怎样转动,两个正方形重叠部分的面积,总等于一个正方形面积的( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |
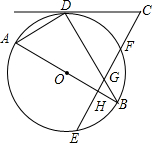 如图,AB是⊙O的直径,BD,EF是⊙O的弦,EF⊥AB于点H,交BD于点G,过点D的直线与EF的延长线交于点C,若△CDG是等边三角形.
如图,AB是⊙O的直径,BD,EF是⊙O的弦,EF⊥AB于点H,交BD于点G,过点D的直线与EF的延长线交于点C,若△CDG是等边三角形.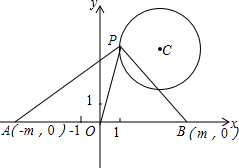 在平面直角坐标系xOy中,A(-m,0),B(m,0)(其中m>0),点P在以点C(3,4)为圆心,半径等于2的圆上,如果动点P满足∠APB=90°,
在平面直角坐标系xOy中,A(-m,0),B(m,0)(其中m>0),点P在以点C(3,4)为圆心,半径等于2的圆上,如果动点P满足∠APB=90°,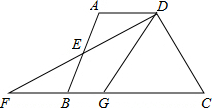 如图,在四边形ABCD中,AD∥BC,E是AB的中点,连接DE并延长交CB的延长线于点F,点G在边BC上,且∠GDF=∠ADF.
如图,在四边形ABCD中,AD∥BC,E是AB的中点,连接DE并延长交CB的延长线于点F,点G在边BC上,且∠GDF=∠ADF.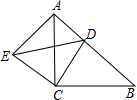 如图,已知△ABC和△ECD都是等腰直角三角形,∠ACB=∠DCE=90°,点D为AB边上一点.
如图,已知△ABC和△ECD都是等腰直角三角形,∠ACB=∠DCE=90°,点D为AB边上一点.