题目内容
3.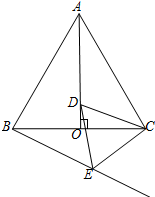 如图,等边△ABC的边长为6,AO⊥BC于D,D为AO上一点,以CD为一边且在CD下方作等边△CDE,连结BE.
如图,等边△ABC的边长为6,AO⊥BC于D,D为AO上一点,以CD为一边且在CD下方作等边△CDE,连结BE.(1)求证:点D在线段BE的垂直平分线上;
(2)求∠CBE的度数;
(3)求点C到直线BE的距离.
分析 (1)连结BD,由等边△ABC中,AO⊥BC,得到直线AO是BC边的垂直平分线,根据线段垂直平分线的性质得到结论;
(2)由等边三角形的性质和全等三角形的性质即可得到结论;
(3)根据直角三角形的性质,30°角所对的直角边等于斜边的一半.
解答  解:(1)如图1证明:连结BD,
解:(1)如图1证明:连结BD,
∵等边△ABC中,AO⊥BC,
∴直线AO是BC边的垂直平分线,
∴BD=DC,
∵△CDE是等边三角形,即DE=DC,
∴DE=BD,∴点D在线段BE的垂直平分线上;
(2)∵△ABC和△CDE均为等边三角形,
∴AC=BC,CD=CE,∠ACB=∠DCE=60°,
∴∠ACD+∠DCB=∠DCB+∠BCE=60°,
∴∠ACD=∠BCE,
在△ACD与△BCE中,$\left\{\begin{array}{l}{AC=BC}\\{∠ACD=∠BCE}\\{CD=CE}\end{array}\right.$,
∴△ACD≌△BCE,
∴∠CBE=∠CAD,
∵在等边△ABC中,AO⊥BC,
∴AO是∠BAC的角平分线,即∠CAD=∠CBE=30°;
(3)如图2过点C作CG⊥BE,交BE的延长线于G,
∴在△CBE中,∠CBE=30°,
∴CG=$\frac{1}{2}$CB=3.
点评 此题考查了全等三角形的判定与性质、等边三角形的性质、等腰三角形的性质以及含30°角的直角三角形的性质.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.方程:$\frac{2}{x}$+$\frac{3}{{x}^{2}}$=1的解是( )
| A. | x=-1 | B. | x=3 | C. | x=-1或x=3 | D. | x=1或x=-312 |
13.下列事件中,为必然事件的是( )
| A. | 购买一张彩票,中奖 | |
| B. | 一个袋中只装有2个黑球,从中摸出一个球是黑球 | |
| C. | 抛掷一枚硬币,正面向上 | |
| D. | 打开电视,正在播放广告 |
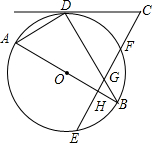 如图,AB是⊙O的直径,BD,EF是⊙O的弦,EF⊥AB于点H,交BD于点G,过点D的直线与EF的延长线交于点C,若△CDG是等边三角形.
如图,AB是⊙O的直径,BD,EF是⊙O的弦,EF⊥AB于点H,交BD于点G,过点D的直线与EF的延长线交于点C,若△CDG是等边三角形.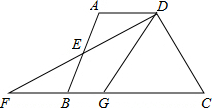 如图,在四边形ABCD中,AD∥BC,E是AB的中点,连接DE并延长交CB的延长线于点F,点G在边BC上,且∠GDF=∠ADF.
如图,在四边形ABCD中,AD∥BC,E是AB的中点,连接DE并延长交CB的延长线于点F,点G在边BC上,且∠GDF=∠ADF.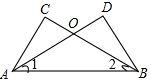 已知如图,在△ABC和△ABD中,AD和BC交于点O,∠1=∠2,请你添加一个条件∠C=∠D(不再添加其它线段,不再标注或使用其它字母),使AC=BD.
已知如图,在△ABC和△ABD中,AD和BC交于点O,∠1=∠2,请你添加一个条件∠C=∠D(不再添加其它线段,不再标注或使用其它字母),使AC=BD. 如图,已知△ABC和△ECD都是等腰直角三角形,∠ACB=∠DCE=90°,点D为AB边上一点.
如图,已知△ABC和△ECD都是等腰直角三角形,∠ACB=∠DCE=90°,点D为AB边上一点.