题目内容
 如图,已知BC为半圆O的直径,
如图,已知BC为半圆O的直径, |
| AB |
 |
| AF |
(1)若∠FBC=α,求∠ACB的度数(用α表示);
(2)过点A作AD⊥BC于D,交BF于E,求证:BE=EM.
考点:圆周角定理,等腰三角形的判定与性质
专题:
分析:(1)先由BC为半圆O的直径,根据圆周角定理得出AB⊥AC,那么∠ABF+∠FBC+∠ACB=90°①,再由
=
,根据圆周角定理得出∠ABF=∠ACB,代入①得2∠ACB+∠FBC=90°,再将∠FBC=α代入,即可求出∠ACB=45°-
α;
(2)先证明BE=AE,再证明EM=AE,即可证明BE=EM.
 |
| AB |
 |
| AF |
| 1 |
| 2 |
(2)先证明BE=AE,再证明EM=AE,即可证明BE=EM.
解答:解:(1)∵BC是直径,
∴AB⊥AC,
∴∠ABF+∠FBC+∠ACB=90°.
∵弧AB=弧AF,
∴∠ABF=∠ACB,
∴2∠ACB+∠FBC=90°,
又∠FBC=α,
∴2∠ACB+α=90°,
∴∠ACB=45°-
α;
 (2)∵AB⊥AC,AD⊥BC,
(2)∵AB⊥AC,AD⊥BC,
∴∠BAE=∠ACB.
∵∠ABF=∠ACB,
∴∠BAE=∠ABF,
∴BE=AE.
∵∠AME=90°-∠ABF,∠EAM=90°-∠ACB,而∠ABF=∠ACB,
∴∠AME=∠EAM,
∴EM=AE.
∴BE=EM.
∴AB⊥AC,
∴∠ABF+∠FBC+∠ACB=90°.
∵弧AB=弧AF,
∴∠ABF=∠ACB,
∴2∠ACB+∠FBC=90°,
又∠FBC=α,
∴2∠ACB+α=90°,
∴∠ACB=45°-
| 1 |
| 2 |
 (2)∵AB⊥AC,AD⊥BC,
(2)∵AB⊥AC,AD⊥BC,∴∠BAE=∠ACB.
∵∠ABF=∠ACB,
∴∠BAE=∠ABF,
∴BE=AE.
∵∠AME=90°-∠ABF,∠EAM=90°-∠ACB,而∠ABF=∠ACB,
∴∠AME=∠EAM,
∴EM=AE.
∴BE=EM.
点评:本题考查了圆周角定理,三角形内角和定理,等腰三角形的判定与性质,难度适中.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案
相关题目
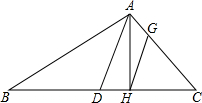 如图,在△ABC中,AD是BC边上的中线,点H在边BC上,且AH=HC,HG∥AD交AC于点G,BD=7,AD=5,DH=3.
如图,在△ABC中,AD是BC边上的中线,点H在边BC上,且AH=HC,HG∥AD交AC于点G,BD=7,AD=5,DH=3.