题目内容
已知在△ABC中,AB=AC,AC边上的中线BD把三角形的周长分为12厘米和18厘米,求△ABC各边的长.
考点:等腰三角形的性质
专题:
分析:等腰三角形一腰上的中线将它的周长分为12厘米和18厘米两部分,但已知没有明确等腰三角形被中线分成的两部分的长,哪个是12厘米,哪个是18厘米,因此,有两种情况,需要分类讨论.
解答: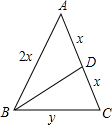 解:根据题意画出图形,如图,
解:根据题意画出图形,如图,
设等腰三角形的腰长AB=AC=2x,BC=y,
∵BD是腰上的中线,
∴AD=DC=x,
若AB+AD的长为12,则2x+x=12,解得x=4,
则x+y=18,即4+y=18,解得y=14;
此时组不成三角形,应舍去.
若AB+AD的长为18,则2x+x=18,解得x=6,
则x+y=12,即6+y=12,解得y=6;
所以等腰三角形的腰长为12厘米,底边长为6厘米.
 解:根据题意画出图形,如图,
解:根据题意画出图形,如图,设等腰三角形的腰长AB=AC=2x,BC=y,
∵BD是腰上的中线,
∴AD=DC=x,
若AB+AD的长为12,则2x+x=12,解得x=4,
则x+y=18,即4+y=18,解得y=14;
此时组不成三角形,应舍去.
若AB+AD的长为18,则2x+x=18,解得x=6,
则x+y=12,即6+y=12,解得y=6;
所以等腰三角形的腰长为12厘米,底边长为6厘米.
点评:本题考查了等腰三角形的性质及三角形三边关系;在解决与等腰三角形有关的问题,由于等腰所具有的特殊性质,很多题目在已知不明确的情况下,要进行分类讨论,才能正确解题,因此,解决和等腰三角形有关的边角问题时,要仔细认真,避免出错;利用三角形三边关系判断能否组成三角形是正确解答本题的关键.

练习册系列答案
相关题目
 如图,已知BC为半圆O的直径,
如图,已知BC为半圆O的直径,
 如图,六边形ABCDEF是⊙O的内接正六边形,P是弧AF上任一点,求
如图,六边形ABCDEF是⊙O的内接正六边形,P是弧AF上任一点,求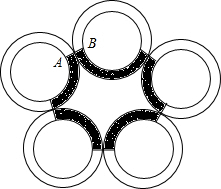 如图是紧密相接的五环,点C为两环的交点,点A与点B分别在两个内环上,且点C在线段AB上,AB=4,阴影部分由五个相同部分组成,若这五环环上空白部分的面积与阴影部分的面积之比为7:3,求阴影部分的周长?(已知大圆半径为5,小圆半径为3)
如图是紧密相接的五环,点C为两环的交点,点A与点B分别在两个内环上,且点C在线段AB上,AB=4,阴影部分由五个相同部分组成,若这五环环上空白部分的面积与阴影部分的面积之比为7:3,求阴影部分的周长?(已知大圆半径为5,小圆半径为3)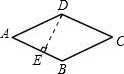 如图,已知菱形ABCD的边长是2,DE⊥AB,垂足为E,∠A=45°,求菱形ABCD的面积.
如图,已知菱形ABCD的边长是2,DE⊥AB,垂足为E,∠A=45°,求菱形ABCD的面积.