题目内容
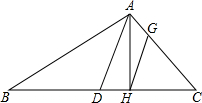 如图,在△ABC中,AD是BC边上的中线,点H在边BC上,且AH=HC,HG∥AD交AC于点G,BD=7,AD=5,DH=3.
如图,在△ABC中,AD是BC边上的中线,点H在边BC上,且AH=HC,HG∥AD交AC于点G,BD=7,AD=5,DH=3.(1)求证:AH⊥BC;
(2)求AG的长.
考点:平行线分线段成比例,勾股定理
专题:
分析:(1)根据三角形的中线的性质,可得DC的长,根据线段的和差,可得HC的长,根据勾股定理的逆定理,可得答案;
(2)根据平行线分线段成比例,可得
=
,根据比例的性质,可得答案.
(2)根据平行线分线段成比例,可得
| CG |
| AC |
| HC |
| CD |
解答:(1)证明:∵AD是BC边上的中线,
∴DC=BD=7,
∵DH+HC=DC=7,
∴HC=DC-DH=7-4=3.
∵AH=HC,
∴AH=CH=3,
∵AH2+DH2=25,AD2=25,
∴AH2+DH2=AD2,
∴∠AHD=90°,
∴AH⊥BC;
(2)设AG=x,
由勾股定理得AC=
=4
,
∵HG∥AD,
=
,即
=
,
解得x=
.
∴DC=BD=7,
∵DH+HC=DC=7,
∴HC=DC-DH=7-4=3.
∵AH=HC,
∴AH=CH=3,
∵AH2+DH2=25,AD2=25,
∴AH2+DH2=AD2,
∴∠AHD=90°,
∴AH⊥BC;
(2)设AG=x,
由勾股定理得AC=
| AH2+HC2 |
| 2 |
∵HG∥AD,
| CG |
| AC |
| HC |
| CD |
4
| ||
4
|
| 3 |
| 7 |
解得x=
16
| ||
| 7 |
点评:本题考查了平行线分线段成比例,利用了勾股定理的逆定理,平行线分线段成比例.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
 如图所示,OE是∠AOB的平分线,OD是∠BOC的平分线,∠AOB=100°,∠EOD=80°,求∠BOC的度数.
如图所示,OE是∠AOB的平分线,OD是∠BOC的平分线,∠AOB=100°,∠EOD=80°,求∠BOC的度数. 如图,已知BC为半圆O的直径,
如图,已知BC为半圆O的直径,
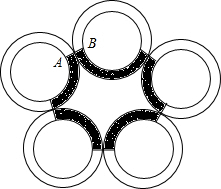 如图是紧密相接的五环,点C为两环的交点,点A与点B分别在两个内环上,且点C在线段AB上,AB=4,阴影部分由五个相同部分组成,若这五环环上空白部分的面积与阴影部分的面积之比为7:3,求阴影部分的周长?(已知大圆半径为5,小圆半径为3)
如图是紧密相接的五环,点C为两环的交点,点A与点B分别在两个内环上,且点C在线段AB上,AB=4,阴影部分由五个相同部分组成,若这五环环上空白部分的面积与阴影部分的面积之比为7:3,求阴影部分的周长?(已知大圆半径为5,小圆半径为3)