题目内容
3. 如图,?ABCD中,AD=10,AB=8,P为BC上的任意一点,E,F,G,H分别为AB,AP,DP,DC的中点,则EF+GH的长是( )
如图,?ABCD中,AD=10,AB=8,P为BC上的任意一点,E,F,G,H分别为AB,AP,DP,DC的中点,则EF+GH的长是( )| A. | 10 | B. | 8 | C. | 5 | D. | 4 |
分析 由?ABCD中,AD=10,AB=8,可得BC=AD=10,然后由E,F,G,H分别为AB,AP,DP,DC的中点,根据三角形中位线的性质,可求得EF+GH=$\frac{1}{2}$BC,继而求得答案.
解答 解:∵四边形ABCD是平行四边形,
∴BC=AD=10,
∵E,F,G,H分别为AB,AP,DP,DC的中点,
∴EF=$\frac{1}{2}$BP,GH=$\frac{1}{2}$CP,
∴EF+GH=$\frac{1}{2}$(BP+CP)=$\frac{1}{2}$BC=5.
故选C.
点评 此题考查了平行四边形的性质以及三角形中位线的性质.注意掌握三角形中位线的性质的应用是解题的关键.

练习册系列答案
相关题目
9.A和B两城市相距420千米,一辆小汽车和一辆客车同时从A、B两地相向开出,经过2.5小时相遇,相遇时,小汽车比客车多行驶70千米,设小汽车和客车的平均速度分别为x千米/小时和y千米/小时,则下列方程组正确的是( )
| A. | $\left\{\begin{array}{l}{x+y=70}\\{2.5x+2.5y=420}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x-y=70}\\{2.5x+2.5y=420}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x+y=70}\\{2.5x-2.5y=420}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{2.5x+2.5y=420}\\{2.5x-2.5y=70}\end{array}\right.$ |
10. 如图,已知∠2=100°,要使AB∥CD,则须具备另一个条件( )
如图,已知∠2=100°,要使AB∥CD,则须具备另一个条件( )
 如图,已知∠2=100°,要使AB∥CD,则须具备另一个条件( )
如图,已知∠2=100°,要使AB∥CD,则须具备另一个条件( )| A. | ∠1=100° | B. | ∠3=80° | C. | ∠4=80° | D. | ∠4=100° |
18.某工厂计划招聘A,B两个工种的工人共180人,月工资额如表所示,若设招聘A种工人的人数为x,所付A,B两个工种的工人总工资为y(元)
(1)写出y与x的函数关系式;
(2)当B工种人数不少于A工种人数的2倍时,那么招聘A工种多少人,可使工厂每月支付的工人总工资最少?最少总工资为多少元?
| 工种 | A | B |
| 月工资(元) | 1500 | 2000 |
(2)当B工种人数不少于A工种人数的2倍时,那么招聘A工种多少人,可使工厂每月支付的工人总工资最少?最少总工资为多少元?
 如图,点G是矩形ABCD的边AD上一点,BG的垂直平分线EF经过点C.如果AG=1,AB=2,那么BC的长等于$\frac{5}{2}$.
如图,点G是矩形ABCD的边AD上一点,BG的垂直平分线EF经过点C.如果AG=1,AB=2,那么BC的长等于$\frac{5}{2}$. 如图,有一块直角三角形纸片,AC=6,BC=8,现将△ABC沿直线AD折叠,使AC落在斜边AB上,且C与点E重合,则AD=3$\sqrt{5}$.
如图,有一块直角三角形纸片,AC=6,BC=8,现将△ABC沿直线AD折叠,使AC落在斜边AB上,且C与点E重合,则AD=3$\sqrt{5}$.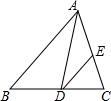 如图,已知AD是△ABC的角平分线,过点D作DE∥AB,交AC于点E,∠B=50°,∠ADE=30°,求∠C的度数.
如图,已知AD是△ABC的角平分线,过点D作DE∥AB,交AC于点E,∠B=50°,∠ADE=30°,求∠C的度数.