题目内容
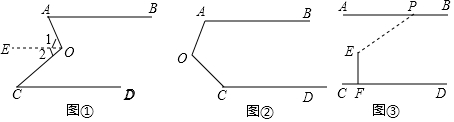
14.如图①,AB∥CD,∠A=65°,∠C=40°.求∠AOC的度数.解:过点O作OE∥AB,
因为AB∥CD,
根据“平行于同一条直线的两条直线平行”,
所以OE∥CD
根据“两条直线平行,内错角相等”,
所以∠1=∠A=65°,∠2=∠C=40°,
所以∠AOC=∠1+∠2=∠A+∠C=65°+40°=105°.
以上解决问题的过程,通过添加一条直线,把要求的角转化为两个角,使问题得到了解决,体现了数学学习中的转化思想,试运用这种思想,解决下面的问题:
(1)如图②,AB∥CD,∠A=112°,∠C=140°,求∠AOC.
(2)如图③,已知AB∥CD,在直线AB上有一光源P,从点P发出的一束光线以与直线AB成32°角射向垂直于CD的标杆EF上的点E处,求∠PEF的度数.
分析 (1)过点O作OE∥AB,由平行线的判定定理得出OE∥CD,再由平行线的性质即可得出结论;
(2)过点E作EG∥AB,则OEG=∠APE=32°,EG∥AB,再由平行线的性质即可得出结论.
解答 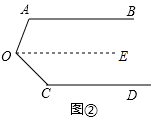 解:(1)如图②,过点O作OE∥AB,
解:(1)如图②,过点O作OE∥AB,
∵AB∥CD,
∴OE∥CD,
∴∠A+∠AOE=180°,∠C+∠COE=180°,
∴∠AOE=180°-∠A=180°-112°=68°,∠COE=180°-∠C=180°-140°=40°,
∴∠AOC=∠AOE+∠COE=68°+40°=108°;
(2)如图③,过点E作EG∥AB,则OEG=∠APE=32°.
∵AB∥CD,EG∥AB,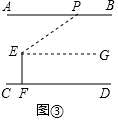
∴EG∥CD,
∴∠GEF+∠EFD=180°.
∵CD⊥EF,
∴∠EFD=90°,
∴∠GEF=90°,
∴∠PEF=∠PEG+∠GEF=32°+90°=122°.
点评 本题考查的是平行线的判定与性质,根据题意作出辅助线,构造出平行线是解答此题的关键.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
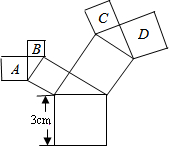 如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为3cm,则图中所有正方形的面积之和为27cm2.
如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为3cm,则图中所有正方形的面积之和为27cm2. 如图所示的是一块矩形ABCD的场地,AB=102m,AD=51m,从A,B两地入口的路宽都为1m,两小路汇合处的路宽为2m,其余部分种植草坪,则草坪的面积为5000m2.
如图所示的是一块矩形ABCD的场地,AB=102m,AD=51m,从A,B两地入口的路宽都为1m,两小路汇合处的路宽为2m,其余部分种植草坪,则草坪的面积为5000m2.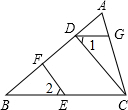 如图,在△ABC中,∠1=∠2,点E、F、G分别在BC、AB、AC上.
如图,在△ABC中,∠1=∠2,点E、F、G分别在BC、AB、AC上.