题目内容
2.设a,b,c,d都是正整数,且a5=b2,c3=d4,a-c=319,则$\frac{b}{{a}^{2}}$-$\frac{c}{d}$=( )| A. | 15 | B. | 17 | C. | 18 | D. | 20 |
分析 设a=m2,b=m5,c=x4,d=x3(m,x为正整数),根据已知a-c=319,运用因式分解的方法得到关于m,x的方程组,从而求解.
解答 解:∵a5=b2,c3=d4,
∴设a=m2,b=m5,c=x4,d=x3(m,x为正整数),
∵a-c=319,
∴m2-x4=319,
即(m+x2)(m-x2)=319,
∴$\left\{\begin{array}{l}{m+{x}^{2}=29}\\{m-{x}^{2}=11}\end{array}\right.$,
解得$\left\{\begin{array}{l}{m=20}\\{{x}^{2}=9}\end{array}\right.$,
则$\frac{b}{{a}^{2}}$-$\frac{c}{d}$=20-3=17.
故选:B.
点评 考查了分式的加减法,此题要注意借助巧妙的设法,运用因式分解的知识达到降次的目的求解.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
 如图,已知面积为1的四边形ABCD内接于⊙O,AC⊥BD,则四边形OABC的面积为$\frac{1}{2}$.
如图,已知面积为1的四边形ABCD内接于⊙O,AC⊥BD,则四边形OABC的面积为$\frac{1}{2}$.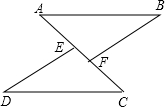 如图,在△ABF与△CDE中,AB=CD,BF=DE,点A、E、F、C在同一条直线上,AE=CF,求证:AB∥CD.
如图,在△ABF与△CDE中,AB=CD,BF=DE,点A、E、F、C在同一条直线上,AE=CF,求证:AB∥CD. 如图,已知:AB⊥DB于点B,CD⊥DB于点D,AB=12,CD=8,BD=28.在DB上是否存在P点,使以C、D、P为顶点的三角形与以P、B、A为顶点的三角形相似?如果存在,计算出点P的位置;如果不存在,请说明理由.
如图,已知:AB⊥DB于点B,CD⊥DB于点D,AB=12,CD=8,BD=28.在DB上是否存在P点,使以C、D、P为顶点的三角形与以P、B、A为顶点的三角形相似?如果存在,计算出点P的位置;如果不存在,请说明理由.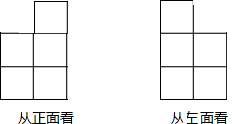 用小立方块搭一个几何体,使得从它的正面和左面看到的形状如图所示.
用小立方块搭一个几何体,使得从它的正面和左面看到的形状如图所示.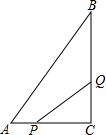 如图所示,在△ABC中,∠C=90°,AC=6cm,BC=8cm,点P从点A出发沿边AC向点C以1cm/s的速度移动,点Q从C点出发沿CB边向点B以2cm/s的速度移动.
如图所示,在△ABC中,∠C=90°,AC=6cm,BC=8cm,点P从点A出发沿边AC向点C以1cm/s的速度移动,点Q从C点出发沿CB边向点B以2cm/s的速度移动. 如图,半圆的半径为r,直角三角形的两条直角边分别为a,b,则图中阴影部分的面积是$\frac{1}{2}$πr2-$\frac{1}{2}$ab.
如图,半圆的半径为r,直角三角形的两条直角边分别为a,b,则图中阴影部分的面积是$\frac{1}{2}$πr2-$\frac{1}{2}$ab.