题目内容
18.直角三角形的周长为12cm,斜边长为5cm,则斜边上的高是2.4cm.分析 根据周长列出关于另外两直角边的关系,再利用勾股定理列出另一关系,联立即可解得两直角边之积,进而可得三角形的面积,再根据面积求斜边上的高.
解答 解:设另外两直角边分别为x,y.
则x+y=12-5=7①,
x2+y2=25②,
①②联立解得xy=12,
故直角三角形的面积$\frac{1}{2}$xy=6,
设斜边上的高为h,则5h×$\frac{1}{2}$=6,
解得:h=2.4,
故答案为:2.4.
点评 此题主要考查了勾股定理,以及直角三角形的面积,关键是根据题意计算出直角三角形的面积.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
9.要登上某建筑物,靠墙有一架梯子,底端离建筑物3m,顶端离地面4m,则梯子的长度为( )
| A. | 2m | B. | 3m | C. | 4m | D. | 5m |
13.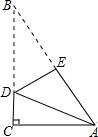 一张直角三角形的纸片,像图中那样折叠,使两个锐角顶点A、B重合,若∠B=30°,AC=$\sqrt{3}$,则折痕DE的长等于( )
一张直角三角形的纸片,像图中那样折叠,使两个锐角顶点A、B重合,若∠B=30°,AC=$\sqrt{3}$,则折痕DE的长等于( )
 一张直角三角形的纸片,像图中那样折叠,使两个锐角顶点A、B重合,若∠B=30°,AC=$\sqrt{3}$,则折痕DE的长等于( )
一张直角三角形的纸片,像图中那样折叠,使两个锐角顶点A、B重合,若∠B=30°,AC=$\sqrt{3}$,则折痕DE的长等于( )| A. | $\sqrt{3}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | 1 | D. | $\frac{\sqrt{2}}{2}$ |
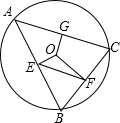 如图,⊙O的半径是$\sqrt{5}$,△ABC是⊙O的内接三角形,过圆心O分别作AB,BC,AC的垂线,垂足为E,F,G,连接EF,若OG=1,则EF的长为2.
如图,⊙O的半径是$\sqrt{5}$,△ABC是⊙O的内接三角形,过圆心O分别作AB,BC,AC的垂线,垂足为E,F,G,连接EF,若OG=1,则EF的长为2. 在如图所示的5×5方格纸中,点A、B在边长为1小正方形的格点上,点C也在正方形的格点上.已知△ABC面积为2,在图中的方格纸中,满足条件的C点有5个.
在如图所示的5×5方格纸中,点A、B在边长为1小正方形的格点上,点C也在正方形的格点上.已知△ABC面积为2,在图中的方格纸中,满足条件的C点有5个.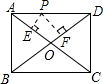 如图,P是矩形的边AD上一个动点,AB、BC的长分别为3和4,那么点P到矩形的两条对角线AC和BD的距离之和是2.4.
如图,P是矩形的边AD上一个动点,AB、BC的长分别为3和4,那么点P到矩形的两条对角线AC和BD的距离之和是2.4.