题目内容
3.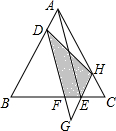 如图,△ABC是正三角形,D,E分别是AB,BC上的点,其中CE=$\frac{1}{4}$CB,以AD,AE为邻边向下作一个平行四边形ADGE,DG交BC于点F,延长GE交AC于点H,连结DH,若S△BDF=9,S△GEF=1那么四边形DFEH的面积为( )
如图,△ABC是正三角形,D,E分别是AB,BC上的点,其中CE=$\frac{1}{4}$CB,以AD,AE为邻边向下作一个平行四边形ADGE,DG交BC于点F,延长GE交AC于点H,连结DH,若S△BDF=9,S△GEF=1那么四边形DFEH的面积为( )| A. | 6 | B. | $\frac{16}{3}$ | C. | $\frac{25}{3}$ | D. | 7 |
分析 由EG∥BD,推出△EFG∽△BFD,得到$\frac{{S}_{△EFG}}{{S}_{△BDF}}$=($\frac{EF}{BF}$)2=$\frac{1}{9}$,所以BF=3EF,再证明EG=EH,由此可以求出△EFH面积,△DFH面积解决问题.
解答 解:如图,连接HF,
设等边三角形ABC边长为4a, ∵四边形ADGE是平行四边形,
∵四边形ADGE是平行四边形,
∴EG∥BD,AD=EG,
∴△EFG∽△BFD
∴$\frac{{S}_{△EFG}}{{S}_{△BDF}}$=($\frac{EF}{BF}$)2=$\frac{1}{9}$,
∴BF=3EF,
∵$\frac{EG}{BD}$=$\frac{FG}{DF}$=$\frac{EF}{BF}$=$\frac{1}{3}$,EC=$\frac{1}{4}$BC=a,
∴AD=EG=EC=a,
∵HE∥AB,
∴∠CEH=∠B=60°,
∴△EHC是等边三角形,
∴EH=EC=EG,
∴S△EFH=S△EFG=1,
∴S△GHF=2,
∴S△DFH=3S△FGH=6,
∴四边形DFEH的面积=S△DFH+S△EFH=7.
故选D.
点评 本题考查平行四边形性质、相似三角形的性质,解题的关键是利用异底同高的两个三角形面积比等于底的比,属于中考填空题中的压轴题.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
13.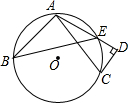 如图,点A,B,C是⊙O上三点,AD和过C点的切线互相垂直,垂足为D,AD交⊙O于点E,若CD=3,AC=5,则cos∠ABE的值为( )
如图,点A,B,C是⊙O上三点,AD和过C点的切线互相垂直,垂足为D,AD交⊙O于点E,若CD=3,AC=5,则cos∠ABE的值为( )
 如图,点A,B,C是⊙O上三点,AD和过C点的切线互相垂直,垂足为D,AD交⊙O于点E,若CD=3,AC=5,则cos∠ABE的值为( )
如图,点A,B,C是⊙O上三点,AD和过C点的切线互相垂直,垂足为D,AD交⊙O于点E,若CD=3,AC=5,则cos∠ABE的值为( )| A. | $\frac{7}{12}$ | B. | $\frac{7}{24}$ | C. | $\frac{24}{25}$ | D. | $\frac{16}{25}$ |

 由于发生山体滑坡灾害,武警救援队火速赶往灾区救援,探测出某建筑物废墟下方点C处有生命迹象.在废墟一侧地面上探测点A、B相距2米,探测线与该面的夹角分别是30°和45°(如图),试确定生命所在点C的深度(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,结果精确到0.1)
由于发生山体滑坡灾害,武警救援队火速赶往灾区救援,探测出某建筑物废墟下方点C处有生命迹象.在废墟一侧地面上探测点A、B相距2米,探测线与该面的夹角分别是30°和45°(如图),试确定生命所在点C的深度(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,结果精确到0.1)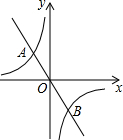 如图,在平面直角坐标系中,反比例函数y=-$\frac{2}{x}$与正比例函数y=kx的图象相交于A、B两点,点A的纵坐标为2.
如图,在平面直角坐标系中,反比例函数y=-$\frac{2}{x}$与正比例函数y=kx的图象相交于A、B两点,点A的纵坐标为2.