题目内容
13.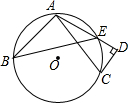 如图,点A,B,C是⊙O上三点,AD和过C点的切线互相垂直,垂足为D,AD交⊙O于点E,若CD=3,AC=5,则cos∠ABE的值为( )
如图,点A,B,C是⊙O上三点,AD和过C点的切线互相垂直,垂足为D,AD交⊙O于点E,若CD=3,AC=5,则cos∠ABE的值为( )| A. | $\frac{7}{12}$ | B. | $\frac{7}{24}$ | C. | $\frac{24}{25}$ | D. | $\frac{16}{25}$ |
分析 作OH⊥AD于D,连结OA、OE,如图,设⊙O的半径为r,先根据勾股定理计算出AD=4,再利用切线的性质可判断OC⊥CD,则可判断四边形OCDH为矩形,所以OH=CD=3,OC=DH=r,接着在Rt△AOH中利用勾股定理得到r2=32+(4-r)2,解得r=$\frac{25}{8}$,于是根据三角函数的定义得cos∠AOH=$\frac{OH}{OA}$=$\frac{24}{25}$,然后根据圆周角定理得到∠ABC=∠AOH,则cos∠ABC=$\frac{24}{25}$.
解答 解:作OH⊥AD于D,连结OA、OE,如图,设⊙O的半径为r,
在Rt△ACD中,AD=$\sqrt{A{C}^{2}-C{D}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4,
∵CD为切线,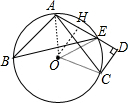
∴OC⊥CD,
∵AD⊥CD,
∴四边形OCDH为矩形,
∴OH=CD=3,OC=DH=r,
∴AH=AD-DH=4-r,
在Rt△AOH中,r2=32+(4-r)2,解得r=$\frac{25}{8}$,
∴cos∠AOH=$\frac{OH}{OA}$=$\frac{3}{\frac{25}{8}}$=$\frac{24}{25}$,
∵OA=OE,OH⊥AE,
∴∠AOH=∠EOH,
∵∠AOE=2∠ABC,
∴∠ABC=∠AOH,
∴cos∠ABC=$\frac{24}{25}$.
故选C.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.简记作:见切点,连半径,见垂直.也考查了勾股定理.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
3.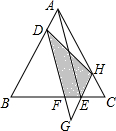 如图,△ABC是正三角形,D,E分别是AB,BC上的点,其中CE=$\frac{1}{4}$CB,以AD,AE为邻边向下作一个平行四边形ADGE,DG交BC于点F,延长GE交AC于点H,连结DH,若S△BDF=9,S△GEF=1那么四边形DFEH的面积为( )
如图,△ABC是正三角形,D,E分别是AB,BC上的点,其中CE=$\frac{1}{4}$CB,以AD,AE为邻边向下作一个平行四边形ADGE,DG交BC于点F,延长GE交AC于点H,连结DH,若S△BDF=9,S△GEF=1那么四边形DFEH的面积为( )
 如图,△ABC是正三角形,D,E分别是AB,BC上的点,其中CE=$\frac{1}{4}$CB,以AD,AE为邻边向下作一个平行四边形ADGE,DG交BC于点F,延长GE交AC于点H,连结DH,若S△BDF=9,S△GEF=1那么四边形DFEH的面积为( )
如图,△ABC是正三角形,D,E分别是AB,BC上的点,其中CE=$\frac{1}{4}$CB,以AD,AE为邻边向下作一个平行四边形ADGE,DG交BC于点F,延长GE交AC于点H,连结DH,若S△BDF=9,S△GEF=1那么四边形DFEH的面积为( )| A. | 6 | B. | $\frac{16}{3}$ | C. | $\frac{25}{3}$ | D. | 7 |
1.在-5,2,-1,3这四个数中,比-2小的数是( )
| A. | -5 | B. | 2 | C. | -1 | D. | 3 |
18.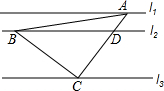 如图,直线l1∥l2∥l3,一等腰直角三角形ABC的三个顶点A,B,C分别在l1,l2,l3上,∠ACB=90°,AC交l2于点D,已知l1与l2的距离为1,l2与l3的距离为3,则$\frac{AB}{BD}$的值为( )
如图,直线l1∥l2∥l3,一等腰直角三角形ABC的三个顶点A,B,C分别在l1,l2,l3上,∠ACB=90°,AC交l2于点D,已知l1与l2的距离为1,l2与l3的距离为3,则$\frac{AB}{BD}$的值为( )
 如图,直线l1∥l2∥l3,一等腰直角三角形ABC的三个顶点A,B,C分别在l1,l2,l3上,∠ACB=90°,AC交l2于点D,已知l1与l2的距离为1,l2与l3的距离为3,则$\frac{AB}{BD}$的值为( )
如图,直线l1∥l2∥l3,一等腰直角三角形ABC的三个顶点A,B,C分别在l1,l2,l3上,∠ACB=90°,AC交l2于点D,已知l1与l2的距离为1,l2与l3的距离为3,则$\frac{AB}{BD}$的值为( )| A. | $\frac{4\sqrt{2}}{5}$ | B. | $\frac{\sqrt{34}}{5}$ | C. | $\frac{5\sqrt{2}}{8}$ | D. | $\frac{20\sqrt{2}}{23}$ |
3.甲、乙两名队员参加射击训练,成绩分别被制成下列两个统计图:

根据以上信息,整理分析数据如下:
(1)写出表格中a,b,c的值;
(2)分别运用表中的四个统计量,简要分析这两名队员的射击训练成绩.若选派其中一名参赛,你认为应选哪名队员?

根据以上信息,整理分析数据如下:
| 平均成绩/环 | 中位数/环 | 众数/环 | 方差 | |
| 甲 | a | 7 | 7 | 1.2 |
| 乙 | 7 | b | 8 | c |
(2)分别运用表中的四个统计量,简要分析这两名队员的射击训练成绩.若选派其中一名参赛,你认为应选哪名队员?
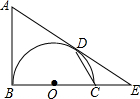 如图,AB是以BC为直径的半圆O的切线,D为半圆上一点,AD=AB,AD,BC的延长线相交于点E.
如图,AB是以BC为直径的半圆O的切线,D为半圆上一点,AD=AB,AD,BC的延长线相交于点E.