题目内容
8.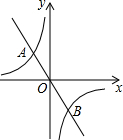 如图,在平面直角坐标系中,反比例函数y=-$\frac{2}{x}$与正比例函数y=kx的图象相交于A、B两点,点A的纵坐标为2.
如图,在平面直角坐标系中,反比例函数y=-$\frac{2}{x}$与正比例函数y=kx的图象相交于A、B两点,点A的纵坐标为2.(1)求正比例函数的表达式及点B的坐标;
(2)结合图象直接写出当kx>-$\frac{2}{x}$时,x的取值范围是x<-1或0<x1.
分析 (1)先确定点A坐标,根据待定系数法可以求出正比例函数解析式,然后根据关于原点对称求出点B坐标即可.
(2)根据正比例函数图象在反比例函数图象的上方,即可确定自变量x的取值范围.
解答 解:(1)∵反比例函数y=-$\frac{2}{x}$的图象经过点A,点A的纵坐标为2,
∴2=-$\frac{2}{x}$,
∴x=-1,
∴点A的坐标为(-1,2).
∵点A与点B关于原点对称,
∴点B的坐标为(1,-2).
把A(-1,2)代入y=kx中,得k=-2.
∴正比例函数的表达式为y=-2.
(2)由图象可知当kx>-$\frac{2}{x}$时,x<-1或0<x<1.
故答案为x<-1或0<x<1.
点评 本题考查一次函数与反比例函数的图象的交点,解题的关键是熟练掌握待定系数法确定函数解析式,学会利用图象确定自变量x取值范围,属于中考常考题型.

练习册系列答案
相关题目
18. 某区对即将参加中考的5000名初中毕业生进行了一次视力抽样调查,绘制出频数分布表和频数分布直方图的一部分.
某区对即将参加中考的5000名初中毕业生进行了一次视力抽样调查,绘制出频数分布表和频数分布直方图的一部分.
请根据图表信息回答下列问题:
(1)本次调查的样本为200名初中毕业生的视力情况,样本容量为200;
(2)在频数分布表中,a=60,b=0.05,并将频数分布直方图补充完整;
(3)若视力在4.6以上(含4.6)均属正常,根据上述信息估计全区初中毕业生中视力正常的学生有多少人?
 某区对即将参加中考的5000名初中毕业生进行了一次视力抽样调查,绘制出频数分布表和频数分布直方图的一部分.
某区对即将参加中考的5000名初中毕业生进行了一次视力抽样调查,绘制出频数分布表和频数分布直方图的一部分.请根据图表信息回答下列问题:
| 视力 | 频数(人) | 频率 |
| 4.0≤x<4.3 | 20 | 0.1 |
| 4.3≤x<4.6 | 40 | 0.2 |
| 4.6≤x<4.9 | 70 | 0.35 |
| 4.9≤x<5.2 | a | 0.3 |
| 5.2≤x<5.5 | 10 | b |
(2)在频数分布表中,a=60,b=0.05,并将频数分布直方图补充完整;
(3)若视力在4.6以上(含4.6)均属正常,根据上述信息估计全区初中毕业生中视力正常的学生有多少人?
3.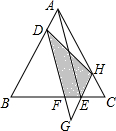 如图,△ABC是正三角形,D,E分别是AB,BC上的点,其中CE=$\frac{1}{4}$CB,以AD,AE为邻边向下作一个平行四边形ADGE,DG交BC于点F,延长GE交AC于点H,连结DH,若S△BDF=9,S△GEF=1那么四边形DFEH的面积为( )
如图,△ABC是正三角形,D,E分别是AB,BC上的点,其中CE=$\frac{1}{4}$CB,以AD,AE为邻边向下作一个平行四边形ADGE,DG交BC于点F,延长GE交AC于点H,连结DH,若S△BDF=9,S△GEF=1那么四边形DFEH的面积为( )
 如图,△ABC是正三角形,D,E分别是AB,BC上的点,其中CE=$\frac{1}{4}$CB,以AD,AE为邻边向下作一个平行四边形ADGE,DG交BC于点F,延长GE交AC于点H,连结DH,若S△BDF=9,S△GEF=1那么四边形DFEH的面积为( )
如图,△ABC是正三角形,D,E分别是AB,BC上的点,其中CE=$\frac{1}{4}$CB,以AD,AE为邻边向下作一个平行四边形ADGE,DG交BC于点F,延长GE交AC于点H,连结DH,若S△BDF=9,S△GEF=1那么四边形DFEH的面积为( )| A. | 6 | B. | $\frac{16}{3}$ | C. | $\frac{25}{3}$ | D. | 7 |
13.计算(-4)+(-9)的结果是( )
| A. | -13 | B. | -5 | C. | 5 | D. | 13 |
18.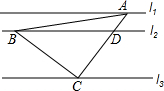 如图,直线l1∥l2∥l3,一等腰直角三角形ABC的三个顶点A,B,C分别在l1,l2,l3上,∠ACB=90°,AC交l2于点D,已知l1与l2的距离为1,l2与l3的距离为3,则$\frac{AB}{BD}$的值为( )
如图,直线l1∥l2∥l3,一等腰直角三角形ABC的三个顶点A,B,C分别在l1,l2,l3上,∠ACB=90°,AC交l2于点D,已知l1与l2的距离为1,l2与l3的距离为3,则$\frac{AB}{BD}$的值为( )
 如图,直线l1∥l2∥l3,一等腰直角三角形ABC的三个顶点A,B,C分别在l1,l2,l3上,∠ACB=90°,AC交l2于点D,已知l1与l2的距离为1,l2与l3的距离为3,则$\frac{AB}{BD}$的值为( )
如图,直线l1∥l2∥l3,一等腰直角三角形ABC的三个顶点A,B,C分别在l1,l2,l3上,∠ACB=90°,AC交l2于点D,已知l1与l2的距离为1,l2与l3的距离为3,则$\frac{AB}{BD}$的值为( )| A. | $\frac{4\sqrt{2}}{5}$ | B. | $\frac{\sqrt{34}}{5}$ | C. | $\frac{5\sqrt{2}}{8}$ | D. | $\frac{20\sqrt{2}}{23}$ |
