题目内容
12．
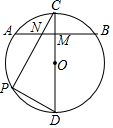如图，CD为⊙O的直径，弦AB交CD于点M，M是AB的中点，点P在$\widehat{AD}$上，PC与AB交于点N，∠PNA=60°，则∠PDC等于（ ）| A． | 40° | B． | 50° | C． | 60° | D． | 70° |
分析 先根据圆周角定理得出∠P=90°，再由M是AB的中点可知CM⊥AB，由∠PNA=60°得出∠C的度数，进而可得出结论．
解答 解：∵CD为⊙O的直径，
∴∠P=90°．
∵M是AB的中点，
∴CM⊥AB．
∵∠PNA=60°，
∴∠C=90°-60°=30°，
∴∠PDC=90°-∠C=90°-30°=60°．
故选C．
点评 本题考查的是圆周角定理，熟知直径所对的圆周角是直角是解答此题的关键．
练习册系列答案
口算心算速算应用题系列答案
同步拓展阅读系列答案
相关题目
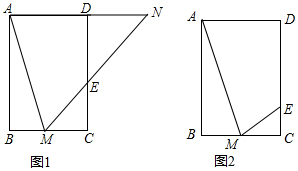
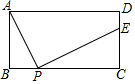如图，矩形ABCD中，AB=4，BC=m（m＞0）．P为边BC上一动点（不与B、C重合），过P点作PE⊥AP交直线CD于E．
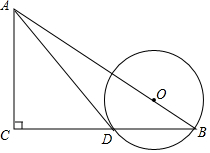如图，在Rt△ABC中，∠ACB=Rt∠，点O在斜边AB上，以OB的长为半径的⊙O与BC交于点D，且AD与⊙O相切于点D．
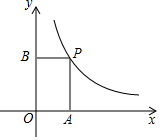已知如图，在平面直角坐标系中，点P是反比例函数y=$\frac{{k}^{2}}{x}$（x＞0）的图象上的一点，分别过P作PA⊥x轴于点A，PB⊥y轴于点B，若四边形OAPB的面积为4，则k值为（ ）