题目内容
3.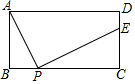 如图,矩形ABCD中,AB=4,BC=m(m>0).P为边BC上一动点(不与B、C重合),过P点作PE⊥AP交直线CD于E.
如图,矩形ABCD中,AB=4,BC=m(m>0).P为边BC上一动点(不与B、C重合),过P点作PE⊥AP交直线CD于E.(1)求证:△ABP∽△PCE;
(2)当P为BC中点时,E恰好为CD的中点,求m的值;
(3)若m=12,DE=1,求BP的长.
分析 (1)根据∠B=90°,PE⊥AP,即可得到∠BAP=∠CPE,再根据∠B=∠C=90°,即可得出△ABP∽△PCE;
(2)当P为BC中点时,E恰好为CD的中点时,BP=CP=$\frac{1}{2}$m,CE=2,根据△ABP∽△PCE,可得$\frac{BP}{CE}$=$\frac{AB}{PC}$,进而得到$\frac{\frac{1}{2}m}{2}$=$\frac{4}{\frac{1}{2}m}$,据此可得m的值为$4\sqrt{2}$;
(3)设BP的长为x,根据△ABP∽△PCE,可得$\frac{AB}{PC}=\frac{BP}{CE}$,再分两种情况进行讨论:当点E在线段CD上时,CE=2,当点E在CD的延长线上时,CE=5,分别求得BP的长.
解答  解:(1)∵矩形ABCD中,∠B=90°,PE⊥AP,
解:(1)∵矩形ABCD中,∠B=90°,PE⊥AP,
∴∠BAP+∠APB=90°,∠CPE+∠APB=90°,
∴∠BAP=∠CPE,
又∵∠B=∠C=90°,
∴△ABP∽△PCE;
(2)当P为BC中点时,E恰好为CD的中点时,BP=CP=$\frac{1}{2}$m,CE=2,
∵△ABP∽△PCE,
∴$\frac{BP}{CE}$=$\frac{AB}{PC}$,
∴$\frac{\frac{1}{2}m}{2}$=$\frac{4}{\frac{1}{2}m}$,
解得m1=4$\sqrt{2}$,m2=-4$\sqrt{2}$(舍去),
∴m的值为$4\sqrt{2}$;
(3)设BP的长为x,
∵△ABP∽△PCE,
∴$\frac{AB}{PC}=\frac{BP}{CE}$,
当点E在线段CD上时,CE=2,
∴$\frac{4}{12-x}=\frac{x}{3}$
解得x1=$6+2\sqrt{6}$,x2=$6-2\sqrt{6}$;
当点E在CD的延长线上时,CE=5,
∴$\frac{4}{12-x}=\frac{x}{5}$,
解得x3=2,x4=10,
∴BP的长为$6+2\sqrt{6}$,$6-2\sqrt{6}$,2,10.
点评 本题属于四边形综合题,主要考查了相似三角形的判定与性质,矩形的性质的运用,解题时注意分类思想的运用.解决问题的关键是掌握:有两组角对应相等的两个三角形相似.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 一个几何体的主视图和俯视图如图所示,那么它的左视图可能是( )
一个几何体的主视图和俯视图如图所示,那么它的左视图可能是( )



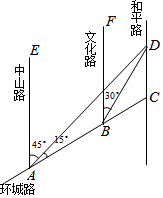 如图,AC是某市环城路的一段,AE,BF,CD都是南北方向的街道,其与环城路AC的交叉路口分别是A,B,C,经测量,花卉世界D位于点A的北偏东45°方向,点B的北偏东30°方向上,AB=2km,∠DAC=15°.
如图,AC是某市环城路的一段,AE,BF,CD都是南北方向的街道,其与环城路AC的交叉路口分别是A,B,C,经测量,花卉世界D位于点A的北偏东45°方向,点B的北偏东30°方向上,AB=2km,∠DAC=15°. 如图,△ABC内接于⊙O,直径AB=8,D为BA延长线上一点且AD=4,E为线段CD上一点,满足∠EAC=∠BAC,则AE=2.
如图,△ABC内接于⊙O,直径AB=8,D为BA延长线上一点且AD=4,E为线段CD上一点,满足∠EAC=∠BAC,则AE=2.
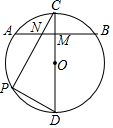 如图,CD为⊙O的直径,弦AB交CD于点M,M是AB的中点,点P在$\widehat{AD}$上,PC与AB交于点N,∠PNA=60°,则∠PDC等于( )
如图,CD为⊙O的直径,弦AB交CD于点M,M是AB的中点,点P在$\widehat{AD}$上,PC与AB交于点N,∠PNA=60°,则∠PDC等于( )