题目内容
17.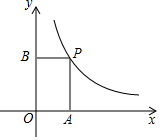 已知如图,在平面直角坐标系中,点P是反比例函数y=$\frac{{k}^{2}}{x}$(x>0)的图象上的一点,分别过P作PA⊥x轴于点A,PB⊥y轴于点B,若四边形OAPB的面积为4,则k值为( )
已知如图,在平面直角坐标系中,点P是反比例函数y=$\frac{{k}^{2}}{x}$(x>0)的图象上的一点,分别过P作PA⊥x轴于点A,PB⊥y轴于点B,若四边形OAPB的面积为4,则k值为( )| A. | 2 | B. | ±2 | C. | 4 | D. | -4 |
分析 根据矩形OAPB的面积结合反比例函数系数k的几何意义即可得出k2=4,解之即可得出结论.
解答 解:∵点P是反比例函数y=$\frac{{k}^{2}}{x}$(x>0)的图象上的一点,分别过P作PA⊥x轴于点A,PB⊥y轴于点B,若四边形OAPB的面积为4,
∴k2=4,
解得:k=±2.
故选B.
点评 本题考查了反比例函数系数k的几何意义,熟练掌握“在反比例函数y=xk图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|”是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
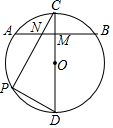 如图,CD为⊙O的直径,弦AB交CD于点M,M是AB的中点,点P在$\widehat{AD}$上,PC与AB交于点N,∠PNA=60°,则∠PDC等于( )
如图,CD为⊙O的直径,弦AB交CD于点M,M是AB的中点,点P在$\widehat{AD}$上,PC与AB交于点N,∠PNA=60°,则∠PDC等于( )



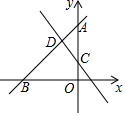 如图,直线y=kx+4(k≠0)与x轴,y轴分别交于点B,A,直线y=-2x+1与y轴交于点C,与直线y=kx+4交于点D,△ACD的面积$\frac{3}{2}$.
如图,直线y=kx+4(k≠0)与x轴,y轴分别交于点B,A,直线y=-2x+1与y轴交于点C,与直线y=kx+4交于点D,△ACD的面积$\frac{3}{2}$. 已知:如图,在△ABC中,M是边AB的中点,D是边BC延长线上的一点,且CD=$\frac{1}{2}$BC,作DN∥CM交AC于点N.
已知:如图,在△ABC中,M是边AB的中点,D是边BC延长线上的一点,且CD=$\frac{1}{2}$BC,作DN∥CM交AC于点N.