题目内容
7.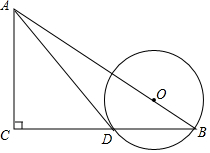 如图,在Rt△ABC中,∠ACB=Rt∠,点O在斜边AB上,以OB的长为半径的⊙O与BC交于点D,且AD与⊙O相切于点D.
如图,在Rt△ABC中,∠ACB=Rt∠,点O在斜边AB上,以OB的长为半径的⊙O与BC交于点D,且AD与⊙O相切于点D.(1)求证:∠CAD=∠ABC;
(2)若tan∠CAD=$\frac{\sqrt{2}}{2}$,BC=2,求⊙O的半径.
分析 (1)连接OD,根据切线的性质可得∠ADO=90°,然后根据直角三角形的两锐角互余以及等腰三角形的性质即可证得;
(2)设AB与圆相交于点E,连接DE,设DE=x,利用△BDE∽△BCA,相似三角形的对应边的比相等即可列方程求得x的值,进而求得半径.
解答 解:(1)证明:连接OD.
∵AD是⊙O的切线,
∴OD⊥AD,即∠ADO=90°.
∴∠ADC+∠ODB=90°,
又∵Rt△ACD中,∠CAD+∠ADC=90°,
∴∠CAD=∠ODB,
又∵OD=OB,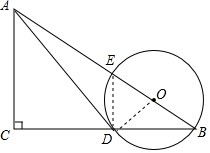
∴∠ODB=∠ABC,
∴∠CAD=∠ABC;
(2)设AB与圆相交于点E,连接DE.
∵BE是⊙O的直径,
∴∠EDB=90°,
∴AC∥DE,
∴△BDE∽△BCA,
∵∠CAD=∠ABC,且tan∠CAD=$\frac{\sqrt{2}}{2}$=$\frac{1}{\sqrt{2}}$,
∴设DE=x,则BD=$\sqrt{2}$x,
∴BE=$\sqrt{D{E}^{2}+B{D}^{2}}$=$\sqrt{3}$x.
∴CD=BC-BD=2-$\sqrt{2}$x.
在Rt△ACD中,tan∠CAD=$\frac{CD}{AC}$=$\frac{\sqrt{2}}{2}$,即$\frac{2-\sqrt{2}x}{AC}$=$\frac{\sqrt{2}}{2}$,
则AC=2$\sqrt{2}$-2x.
∵△BDE∽△BCA,
∴$\frac{DE}{AC}$=$\frac{BD}{BC}$,即$\frac{x}{2\sqrt{2}-2x}$=$\frac{\sqrt{2}x}{2}$,
解得:x=$\frac{\sqrt{2}}{2}$.
则BE=$\frac{\sqrt{6}}{2}$,
则半径是$\frac{1}{2}$BE=$\frac{\sqrt{6}}{4}$.
点评 本题考查了切线的性质以及相似三角形的判定与性质,正确作出辅助线构造相似的三角形是关键.

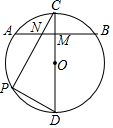 如图,CD为⊙O的直径,弦AB交CD于点M,M是AB的中点,点P在$\widehat{AD}$上,PC与AB交于点N,∠PNA=60°,则∠PDC等于( )
如图,CD为⊙O的直径,弦AB交CD于点M,M是AB的中点,点P在$\widehat{AD}$上,PC与AB交于点N,∠PNA=60°,则∠PDC等于( )| A. | 40° | B. | 50° | C. | 60° | D. | 70° |
 在平面直角坐标系中,若干个半径为2个单位长度,圆心角为60°的扇形组成一条连续的曲线,点P从原点O出发,沿这条曲线向右上下起伏运动,点在直线上的速度为2个单位长度/秒,点在弧线上的速度为$\frac{2π}{3}$个单位长度/秒,则2017秒时,点P的坐标是( )
在平面直角坐标系中,若干个半径为2个单位长度,圆心角为60°的扇形组成一条连续的曲线,点P从原点O出发,沿这条曲线向右上下起伏运动,点在直线上的速度为2个单位长度/秒,点在弧线上的速度为$\frac{2π}{3}$个单位长度/秒,则2017秒时,点P的坐标是( )| A. | (2017,0) | B. | (2017,$\sqrt{3}$) | C. | (2017,-$\sqrt{3}$) | D. | (2016,0) |
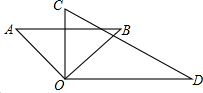 如图,将一副三角板的直角顶点重合,摆放在桌面上,若∠BOC=$\frac{2}{3}$∠AOD,则∠AOD=108°.
如图,将一副三角板的直角顶点重合,摆放在桌面上,若∠BOC=$\frac{2}{3}$∠AOD,则∠AOD=108°. 如图,△ABC内接于⊙O,直径AB=8,D为BA延长线上一点且AD=4,E为线段CD上一点,满足∠EAC=∠BAC,则AE=2.
如图,△ABC内接于⊙O,直径AB=8,D为BA延长线上一点且AD=4,E为线段CD上一点,满足∠EAC=∠BAC,则AE=2.
 张倩同学打算制作一个平行四边形纸板,但手中只有一块等腰三角形纸板.张倩同学想了一下,用剪刀只剪了一刀,便得到一个平行四边形,且纸板充分利用没有浪费.你知道张倩是怎样剪的吗?用虚线表示出剪刀线;并请你画出两种张倩所拼的平行四边形.
张倩同学打算制作一个平行四边形纸板,但手中只有一块等腰三角形纸板.张倩同学想了一下,用剪刀只剪了一刀,便得到一个平行四边形,且纸板充分利用没有浪费.你知道张倩是怎样剪的吗?用虚线表示出剪刀线;并请你画出两种张倩所拼的平行四边形.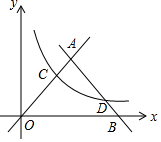 在平面直角坐标系内,双曲线:y=$\frac{k}{x}$(x>0)分别与直线OA:y=x和直线AB:y=-x+10,交于C,D两点,并且OC=3BD.
在平面直角坐标系内,双曲线:y=$\frac{k}{x}$(x>0)分别与直线OA:y=x和直线AB:y=-x+10,交于C,D两点,并且OC=3BD.