题目内容
1.已知坐标平面上有两个二次函数y=a(x+1)(x-7),y=b(x+1)(x-15)的图形,其中a、b为整数.判断将二次函数y=b(x+1)(x-15)的图形依下列哪一种方式平移后,会使得此两图形的对称轴重叠( )| A. | 向左平移4单位 | B. | 向右平移4单位 | C. | 向左平移8单位 | D. | 向右平移8单位 |
分析 将二次函数解析式展开,结合二次函数的性质找出两二次函数的对称轴,二者做差后即可得出平移方向及距离.
解答 解:∵y=a(x+1)(x-7)=ax2-6ax-7a,y=b(x+1)(x-15)=bx2-14bx-15b,
∴二次函数y=a(x+1)(x-7)的对称轴为直线x=3,二次函数y=b(x+1)(x-15)的对称轴为直线x=7,
∵3-7=-4,
∴将二次函数y=b(x+1)(x-15)的图形向左平移4个单位,两图形的对称轴重叠.
故选A.
点评 本题考查了二次函数图象与几何变换以及二次函数的性质,根据二次函数的性质找出两个二次函数的对称轴是解题的关键.

练习册系列答案
相关题目
16. 为了解六年级学生的课外作业情况,某学校从该年级学生中随机抽取了若干名学生,对他们的课外作业时间(单位:min)进行调查,并将收集的数据整理绘制成如下两幅不完整的图表,请根据图中信息,解答下列问题:
为了解六年级学生的课外作业情况,某学校从该年级学生中随机抽取了若干名学生,对他们的课外作业时间(单位:min)进行调查,并将收集的数据整理绘制成如下两幅不完整的图表,请根据图中信息,解答下列问题:
(1)本次调查共抽取了50名学生,a=20,b=3;
(2)求出作业时间为75~90min的部分对应的扇形圆心角的度数;
(3)请根据上表绘制频数直方图.
 为了解六年级学生的课外作业情况,某学校从该年级学生中随机抽取了若干名学生,对他们的课外作业时间(单位:min)进行调查,并将收集的数据整理绘制成如下两幅不完整的图表,请根据图中信息,解答下列问题:
为了解六年级学生的课外作业情况,某学校从该年级学生中随机抽取了若干名学生,对他们的课外作业时间(单位:min)进行调查,并将收集的数据整理绘制成如下两幅不完整的图表,请根据图中信息,解答下列问题:| 课外作业时间 (分组) | 人数 (频数) |
| 30~45 | 5 |
| 45~60 | 12 |
| 60~75 | a |
| 75~90 | 10 |
| 90~105 | b |
(2)求出作业时间为75~90min的部分对应的扇形圆心角的度数;
(3)请根据上表绘制频数直方图.
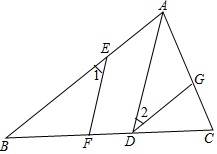 已知:如图,点D、E、G分别是△ABC边BC、AB和AC上的点,AD∥EF,点F在BC上,∠1=∠2=∠B.
已知:如图,点D、E、G分别是△ABC边BC、AB和AC上的点,AD∥EF,点F在BC上,∠1=∠2=∠B. 如图,EN⊥CD,点M在AB上,∠MEN=156°,当∠BME=66°时,AB∥CD.
如图,EN⊥CD,点M在AB上,∠MEN=156°,当∠BME=66°时,AB∥CD. 如图,在四边形ABCD中,AB∥CD,AB⊥BC,则∠DCB=90°.
如图,在四边形ABCD中,AB∥CD,AB⊥BC,则∠DCB=90°.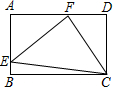 如图,E、F分别是矩形ABCD的边AB、AD上的点,∠FEC=∠FCE=45°
如图,E、F分别是矩形ABCD的边AB、AD上的点,∠FEC=∠FCE=45°
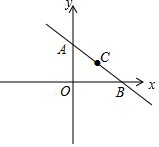 如图,直线y=-$\frac{3}{4}$x+6与坐标轴交于A、B两点.点C在此直线上且横坐标为4.点D为y轴上一动点.当以点O、B、C、D为顶点的四边形为梯形时.点D的坐标为(0,3).
如图,直线y=-$\frac{3}{4}$x+6与坐标轴交于A、B两点.点C在此直线上且横坐标为4.点D为y轴上一动点.当以点O、B、C、D为顶点的四边形为梯形时.点D的坐标为(0,3).