题目内容
12.若a>0,且ax=3,ay=2,则ax-2y=$\frac{3}{4}$.分析 逆运用同底数幂相除,底数不变指数相减和幂的乘方,底数不变指数相乘进行计算即可得解.
解答 解:∵ax=3,ay=2,
∴ax-2y=ax÷a2y=ax÷(ay)2=3÷22=$\frac{3}{4}$.
故答案为:$\frac{3}{4}$.
点评 本题考查了同底数幂的除法,幂的乘方和积的乘方的性质,熟练掌握运算性质和法则是解题的关键.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
1.已知坐标平面上有两个二次函数y=a(x+1)(x-7),y=b(x+1)(x-15)的图形,其中a、b为整数.判断将二次函数y=b(x+1)(x-15)的图形依下列哪一种方式平移后,会使得此两图形的对称轴重叠( )
| A. | 向左平移4单位 | B. | 向右平移4单位 | C. | 向左平移8单位 | D. | 向右平移8单位 |
 如图,由若干个棱长相同的小正方体堆成的几何体,请画出从正面、左面、上面看到的几何体的形状图.
如图,由若干个棱长相同的小正方体堆成的几何体,请画出从正面、左面、上面看到的几何体的形状图.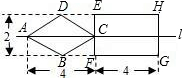 如图,直线l是菱形ABCD和矩形EFGH的对称轴,点C在EF边上,若菱形ABCD沿直线l从左向右匀速运动直至点C落在GH边上停止运动.能反映菱形进入矩形内部的周长y与运动的时间x之间关系的图象大致是( )
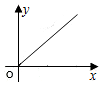
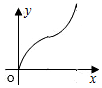
如图,直线l是菱形ABCD和矩形EFGH的对称轴,点C在EF边上,若菱形ABCD沿直线l从左向右匀速运动直至点C落在GH边上停止运动.能反映菱形进入矩形内部的周长y与运动的时间x之间关系的图象大致是( )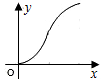
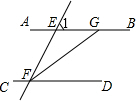 如图,AB∥CD,∠EFG=∠EGF,∠BGF=146°,则∠1的度数为68°.
如图,AB∥CD,∠EFG=∠EGF,∠BGF=146°,则∠1的度数为68°.