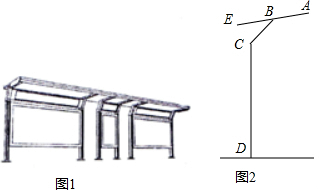
题目内容
1．
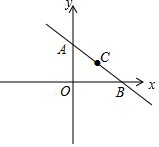如图，直线y=-$\frac{3}{4}$x+6与坐标轴交于A、B两点．点C在此直线上且横坐标为4．点D为y轴上一动点．当以点O、B、C、D为顶点的四边形为梯形时．点D的坐标为（0，3）．
分析 有点D在y轴上结合梯形的定义，即可得出CD∥OB，由点C的横坐标利用一次函数图象上点的坐标特征可得出点C的坐标，由CD∥x轴即可得出点D的坐标．
解答 解：∵点D为y轴上一动点，
∴OD在y轴上，
∴BC和OD不平行．
∵四边形OBCD为梯形，
∴CD∥OB．
过点C作CD⊥y轴，垂足为点D，
当x=4时，y=-$\frac{3}{4}$x+6=3，
∴点C的坐标为（4，3），
∴点D的坐标为（0，3）．
故答案为：（0，3）．
点评 本题考查了一次函数图象上点的坐标特征以及梯形，根据梯形的定义找出CD∥x轴是解题的关键．
练习册系列答案
优百分课时互动系列答案
相关题目
1．已知坐标平面上有两个二次函数y=a（x+1）（x-7），y=b（x+1）（x-15）的图形，其中a、b为整数．判断将二次函数y=b（x+1）（x-15）的图形依下列哪一种方式平移后，会使得此两图形的对称轴重叠（ ）
| A． | 向左平移4单位 | B． | 向右平移4单位 | C． | 向左平移8单位 | D． | 向右平移8单位 |
16．以$\frac{1+\sqrt{3}}{2}$和$\frac{-1+\sqrt{3}}{2}$为根的一个一元二次方程是（ ）
| A． | x2-$\sqrt{3}$x+$\frac{1}{2}$=0 | B． | x2+$\sqrt{3}$x+$\frac{1}{2}$=0 | C． | x2-$\sqrt{3}$x+1=0 | D． | x2+$\sqrt{3}$x-$\frac{1}{2}$=0 |
13．
甲骑摩托车从A地去B地．乙开汽车从B地去A地．同时出发，匀速行驶．各自到达终点后停止．设甲、乙两人间的距离为s（单位：千米），甲行驶的时间为t（单位：小时），s与t之间的函数关系如图所示，下列结论中，错误的是（ ）
甲骑摩托车从A地去B地．乙开汽车从B地去A地．同时出发，匀速行驶．各自到达终点后停止．设甲、乙两人间的距离为s（单位：千米），甲行驶的时间为t（单位：小时），s与t之间的函数关系如图所示，下列结论中，错误的是（ ）| A． | 出发1小时时，甲、乙在途中相遇 | |
| B． | 出发1.5小时时，乙比甲多行驶了60千米 | |
| C． | 出发3小时时，甲、乙同时到达终点 | |
| D． | 甲的速度是乙速度的一半 |
10．
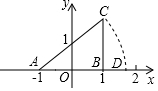如图，Rt△ABC的边AB在x轴上，且A（-1，0），B（1，0），∠A=45°，斜边AC以点A为旋转中心，顺时针旋转45°，恰好与x轴相交于D，则点D的坐标是（ ）
如图，Rt△ABC的边AB在x轴上，且A（-1，0），B（1，0），∠A=45°，斜边AC以点A为旋转中心，顺时针旋转45°，恰好与x轴相交于D，则点D的坐标是（ ）| A． | （$\sqrt{2}$，0） | B． | （2$\sqrt{2}$，0） | C． | （2$\sqrt{2}$-1，0） | D． | （2$\sqrt{2}$-2，0） |