题目内容
10.如图1,在Rt△ABC中,∠ACB=90°,AC=BC,点D、E分别在AC、BC边上,DC=EC,连接DE、AE、BD,点M、N、P分别是AE、BD、AB的中点,连接PM、PN、MN.
(1)BE与MN的数量关系是BE=$\sqrt{2}$MN;
(2)将△DEC绕点C逆时针旋转到如图2的位置,判断(1)中的结论是否仍然成立,如果成立,请写出证明过程,若不成立,请说明理由;
(3)若CB=6,CE=2,在将图1中的△DEC绕点C逆时针旋转一周的过程中,当B、E、D三点在一条直线上时,MN的长度为$\sqrt{17}$-1或$\sqrt{17}$+1.
分析 (1)如图1中,只要证明△PMN的等腰直角三角形,再利用三角形的中位线定理即可解决问题;
(2)如图2中,结论仍然成立.连接AD、延长BE交AD于点H.由△ECB≌△DCA,推出BE=AD,∠DAC=∠EBC,即可推出BH⊥AD,由M、N、P分别为AE、BD、AB的中点,推出PM∥BE,PM=$\frac{1}{2}$BE,PN∥AD,PN=$\frac{1}{2}$AD,推出PM=PN,∠MPN=90°,可得BE=2PM=2×$\frac{\sqrt{2}}{2}$MN=$\sqrt{2}$MN;
(3)有两种情形分别求解即可;
解答 解:(1)如图1中,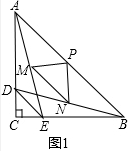
∵AM=ME,AP=PB,
∴PM∥BE,PM=$\frac{1}{2}$BE,
∵BN=DN,AP=PB,
∴PN∥AD,PN=$\frac{1}{2}$AD,
∵AC=BC,CD=CE,
∴AD=BE,
∴PM=PN,
∵∠ACB=90°,
∴AC⊥BC,
∴∵PM∥BC,PN∥AC,
∴PM⊥PN,
∴△PMN的等腰直角三角形,
∴MN=$\sqrt{2}$PM,
∴MN=$\sqrt{2}$•$\frac{1}{2}$BE,
∴BE=$\sqrt{2}$MN,
故答案为BE=$\sqrt{2}$MN.
(2)如图2中,结论仍然成立.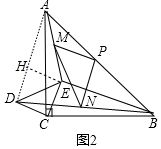
理由:连接AD、延长BE交AD于点H.
∵△ABC和△CDE是等腰直角三角形,
∴CD=CE,CA=CB,∠ACB=∠DCE=90°,
∵∠ACB-∠ACE=∠DCE-∠ACE,
∴∠ACD=∠ECB,
∴△ECB≌△DCA,
∴BE=AD,∠DAC=∠EBC,
∵∠AHB=180°-(∠HAB+∠ABH)
=180°-(45°+∠HAC+∠ABH)
=∠180°-(45°+∠HBC+∠ABH)
=180°-90°
=90°,
∴BH⊥AD,
∵M、N、P分别为AE、BD、AB的中点,
∴PM∥BE,PM=$\frac{1}{2}$BE,PN∥AD,PN=$\frac{1}{2}$AD,
∴PM=PN,∠MPN=90°,
∴BE=2PM=2×$\frac{\sqrt{2}}{2}$MN=$\sqrt{2}$MN.
(3)①如图3中,作CG⊥BD于G,则CE=GE=DG=$\sqrt{2}$,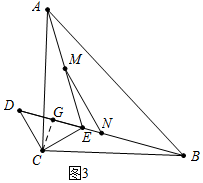
当D、E、B共线时,在Rt△BCG中,BG=$\sqrt{B{C}^{2}-C{G}^{2}}$=$\sqrt{{6}^{2}-(\sqrt{2})^{2}}$=$\sqrt{34}$,
∴BE=BG-GE=$\sqrt{34}$-$\sqrt{2}$,
∴MN=$\frac{\sqrt{2}}{2}$BE=$\sqrt{17}$-1.
②如图4中,作CG⊥BD于G,则CE=GE=DG=$\sqrt{2}$,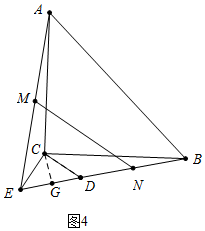
当D、E、B共线时,在Rt△BCG中,BG=$\sqrt{B{C}^{2}-C{G}^{2}}$=$\sqrt{{6}^{2}-(\sqrt{2})^{2}}$=$\sqrt{34}$,
∴BE=BG+GE=$\sqrt{34}$+$\sqrt{2}$,
∴MN=$\frac{\sqrt{2}}{2}$BE=$\sqrt{17}$+1.
故答案为$\sqrt{17}$-1或$\sqrt{17}$+1.
点评 本题考查几何变换综合题、等腰直角三角形的性质、全等三角形的判定和性质、勾股定理等知识,解题的关键是灵活运用所学知识解决问题,学会用分类讨论的思想思考问题,属于中考压轴题.

 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案| A. | 向左平移4单位 | B. | 向右平移4单位 | C. | 向左平移8单位 | D. | 向右平移8单位 |
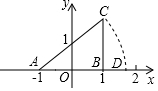 如图,Rt△ABC的边AB在x轴上,且A(-1,0),B(1,0),∠A=45°,斜边AC以点A为旋转中心,顺时针旋转45°,恰好与x轴相交于D,则点D的坐标是( )
如图,Rt△ABC的边AB在x轴上,且A(-1,0),B(1,0),∠A=45°,斜边AC以点A为旋转中心,顺时针旋转45°,恰好与x轴相交于D,则点D的坐标是( )| A. | ($\sqrt{2}$,0) | B. | (2$\sqrt{2}$,0) | C. | (2$\sqrt{2}$-1,0) | D. | (2$\sqrt{2}$-2,0) |
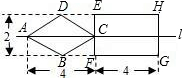 如图,直线l是菱形ABCD和矩形EFGH的对称轴,点C在EF边上,若菱形ABCD沿直线l从左向右匀速运动直至点C落在GH边上停止运动.能反映菱形进入矩形内部的周长y与运动的时间x之间关系的图象大致是( )
如图,直线l是菱形ABCD和矩形EFGH的对称轴,点C在EF边上,若菱形ABCD沿直线l从左向右匀速运动直至点C落在GH边上停止运动.能反映菱形进入矩形内部的周长y与运动的时间x之间关系的图象大致是( )